18 Simple statistical tests

This page demonstrates how to conduct simple statistical tests using base R, rstatix, and gtsummary.

T-test
Shapiro-Wilk test
Wilcoxon rank sum test
Kruskal-Wallis test
Chi-squared test
Correlations between numeric variables

…many other tests can be performed, but we showcase just these common ones and link to further documentation.

Each of the above packages bring certain advantages and disadvantages:

Use base R functions to print a statistical outputs to the R Console
Use rstatix functions to return results in a data frame, or if you want tests to run by group
Use gtsummary if you want to quickly print publication-ready tables

18.1 Preparation

Load packages

This code chunk shows the loading of packages required for the analyses. In this handbook we emphasize p_load() from pacman, which installs the package if necessary and loads it for use. You can also load installed packages with library() from base R. See the page on [R basics] for more information on R packages.

pacman::p_load(
  rio,          # File import
  here,         # File locator
  skimr,        # get overview of data
  tidyverse,    # data management + ggplot2 graphics, 
  gtsummary,    # summary statistics and tests
  rstatix,      # statistics
  corrr,        # correlation analayis for numeric variables
  janitor,      # adding totals and percents to tables
  flextable     # converting tables to HTML
  )

Import data

We import the dataset of cases from a simulated Ebola epidemic. If you want to follow along, click to download the “clean” linelist (as .rds file). Import your data with the import() function from the rio package (it accepts many file types like .xlsx, .rds, .csv - see the [Import and export] page for details).

# import the linelist
linelist <- import("linelist_cleaned.rds")

The first 50 rows of the linelist are displayed below.

18.2 base R

You can use base R functions to conduct statistical tests. The commands are relatively simple and results will print to the R Console for simple viewing. However, the outputs are usually lists and so are harder to manipulate if you want to use the results in subsequent operations.

T-tests

A t-test, also called “Student’s t-Test”, is typically used to determine if there is a significant difference between the means of some numeric variable between two groups. Here we’ll show the syntax to do this test depending on whether the columns are in the same data frame.

Syntax 1: This is the syntax when your numeric and categorical columns are in the same data frame. Provide the numeric column on the left side of the equation and the categorical column on the right side. Specify the dataset to data =. Optionally, set paired = TRUE, and conf.level = (0.95 default), and alternative = (either “two.sided”, “less”, or “greater”). Enter ?t.test for more details.

## compare mean age by outcome group with a t-test
t.test(age_years ~ gender, data = linelist)

## 
##  Welch Two Sample t-test
## 
## data:  age_years by gender
## t = -21.344, df = 4902.3, p-value < 2.2e-16
## alternative hypothesis: true difference in means between group f and group m is not equal to 0
## 95 percent confidence interval:
##  -7.571920 -6.297975
## sample estimates:
## mean in group f mean in group m 
##        12.60207        19.53701

Syntax 2: You can compare two separate numeric vectors using this alternative syntax. For example, if the two columns are in different data sets.

t.test(df1$age_years, df2$age_years)

You can also use a t-test to determine whether a sample mean is significantly different from some specific value. Here we conduct a one-sample t-test with the known/hypothesized population mean as mu =:

t.test(linelist$age_years, mu = 45)

Shapiro-Wilk test

The Shapiro-Wilk test can be used to determine whether a sample came from a normally-distributed population (an assumption of many other tests and analysis, such as the t-test). However, this can only be used on a sample between 3 and 5000 observations. For larger samples a quantile-quantile plot may be helpful.

shapiro.test(linelist$age_years)

Wilcoxon rank sum test

The Wilcoxon rank sum test, also called the Mann–Whitney U test, is often used to help determine if two numeric samples are from the same distribution when their populations are not normally distributed or have unequal variance.

## compare age distribution by outcome group with a wilcox test
wilcox.test(age_years ~ outcome, data = linelist)

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  age_years by outcome
## W = 2501868, p-value = 0.8308
## alternative hypothesis: true location shift is not equal to 0

Kruskal-Wallis test

The Kruskal-Wallis test is an extension of the Wilcoxon rank sum test that can be used to test for differences in the distribution of more than two samples. When only two samples are used it gives identical results to the Wilcoxon rank sum test.

## compare age distribution by outcome group with a kruskal-wallis test
kruskal.test(age_years ~ outcome, linelist)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  age_years by outcome
## Kruskal-Wallis chi-squared = 0.045675, df = 1, p-value = 0.8308

Chi-squared test

Pearson’s Chi-squared test is used in testing for significant differences between categorical croups.

## compare the proportions in each group with a chi-squared test
chisq.test(linelist$gender, linelist$outcome)

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  linelist$gender and linelist$outcome
## X-squared = 0.0011841, df = 1, p-value = 0.9725

18.3 rstatix package

The rstatix package offers the ability to run statistical tests and retrieve results in a “pipe-friendly” framework. The results are automatically in a data frame so that you can perform subsequent operations on the results. It is also easy to group the data being passed into the functions, so that the statistics are run for each group.

Summary statistics

The function get_summary_stats() is a quick way to return summary statistics. Simply pipe your dataset to this function and provide the columns to analyse. If no columns are specified, the statistics are calculated for all columns.

By default, a full range of summary statistics are returned: n, max, min, median, 25%ile, 75%ile, IQR, median absolute deviation (mad), mean, standard deviation, standard error, and a confidence interval of the mean.

linelist %>%
  rstatix::get_summary_stats(age, temp)

## # A tibble: 2 x 13
##   variable     n   min   max median    q1    q3   iqr    mad  mean     sd    se    ci
##   <chr>    <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl> <dbl>  <dbl> <dbl>  <dbl> <dbl> <dbl>
## 1 age       5802   0    84     13     6    23      17 11.9    16.1 12.6   0.166 0.325
## 2 temp      5739  35.2  40.8   38.8  38.2  39.2     1  0.741  38.6  0.977 0.013 0.025

You can specify a subset of summary statistics to return by providing one of the following values to type =: “full”, “common”, “robust”, “five_number”, “mean_sd”, “mean_se”, “mean_ci”, “median_iqr”, “median_mad”, “quantile”, “mean”, “median”, “min”, “max”.

It can be used with grouped data as well, such that a row is returned for each grouping-variable:

linelist %>%
  group_by(hospital) %>%
  rstatix::get_summary_stats(age, temp, type = "common")

## # A tibble: 12 x 11
##    hospital                             variable     n   min   max median   iqr  mean     sd    se    ci
##    <chr>                                <chr>    <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl>
##  1 Central Hospital                     age        445   0    58     12    15    15.7 12.5   0.591 1.16 
##  2 Central Hospital                     temp       450  35.2  40.4   38.8   1    38.5  0.964 0.045 0.089
##  3 Military Hospital                    age        884   0    72     14    18    16.1 12.4   0.417 0.818
##  4 Military Hospital                    temp       873  35.3  40.5   38.8   1    38.6  0.952 0.032 0.063
##  5 Missing                              age       1441   0    76     13    17    16.0 12.9   0.339 0.665
##  6 Missing                              temp      1431  35.8  40.6   38.9   1    38.6  0.97  0.026 0.05 
##  7 Other                                age        873   0    69     13    17    16.0 12.5   0.422 0.828
##  8 Other                                temp       862  35.7  40.8   38.8   1.1  38.5  1.01  0.034 0.067
##  9 Port Hospital                        age       1739   0    68     14    18    16.3 12.7   0.305 0.598
## 10 Port Hospital                        temp      1713  35.5  40.6   38.8   1.1  38.6  0.981 0.024 0.046
## 11 St. Mark's Maternity Hospital (SMMH) age        420   0    84     12    15    15.7 12.4   0.606 1.19 
## 12 St. Mark's Maternity Hospital (SMMH) temp       410  35.9  40.6   38.8   1.1  38.5  0.983 0.049 0.095

You can also use rstatix to conduct statistical tests:

T-test

Use a formula syntax to specify the numeric and categorical columns:

linelist %>% 
  t_test(age_years ~ gender)

## # A tibble: 1 x 10
##   .y.       group1 group2    n1    n2 statistic    df        p    p.adj p.adj.signif
## * <chr>     <chr>  <chr>  <int> <int>     <dbl> <dbl>    <dbl>    <dbl> <chr>       
## 1 age_years f      m       2807  2803     -21.3 4902. 9.89e-97 9.89e-97 ****

Or use ~ 1 and specify mu = for a one-sample T-test. This can also be done by group.

linelist %>% 
  t_test(age_years ~ 1, mu = 30)

## # A tibble: 1 x 7
##   .y.       group1 group2         n statistic    df     p
## * <chr>     <chr>  <chr>      <int>     <dbl> <dbl> <dbl>
## 1 age_years 1      null model  5888     -84.2  5801     0

If applicable, the statistical tests can be done by group, as shown below:

linelist %>% 
  group_by(gender) %>% 
  t_test(age_years ~ 1, mu = 18)

## # A tibble: 3 x 8
##   gender .y.       group1 group2         n statistic    df         p
## * <chr>  <chr>     <chr>  <chr>      <int>     <dbl> <dbl>     <dbl>
## 1 f      age_years 1      null model  2807    -29.8   2806 7.52e-170
## 2 m      age_years 1      null model  2803      5.70  2802 1.34e-  8
## 3 <NA>   age_years 1      null model   278     -3.80   191 1.96e-  4

Shapiro-Wilk test

As stated above, sample size must be between 3 and 5000.

linelist %>% 
  head(500) %>%            # first 500 rows of case linelist, for example only
  shapiro_test(age_years)

## # A tibble: 1 x 3
##   variable  statistic        p
##   <chr>         <dbl>    <dbl>
## 1 age_years     0.917 6.67e-16

Wilcoxon rank sum test

linelist %>% 
  wilcox_test(age_years ~ gender)

## # A tibble: 1 x 9
##   .y.       group1 group2    n1    n2 statistic        p    p.adj p.adj.signif
## * <chr>     <chr>  <chr>  <int> <int>     <dbl>    <dbl>    <dbl> <chr>       
## 1 age_years f      m       2807  2803   2829274 3.47e-74 3.47e-74 ****

Kruskal-Wallis test

Also known as the Mann-Whitney U test.

linelist %>% 
  kruskal_test(age_years ~ outcome)

## # A tibble: 1 x 6
##   .y.           n statistic    df     p method        
## * <chr>     <int>     <dbl> <int> <dbl> <chr>         
## 1 age_years  5888    0.0457     1 0.831 Kruskal-Wallis

Chi-squared test

The chi-square test function accepts a table, so first we create a cross-tabulation. There are many ways to create a cross-tabulation (see Descriptive tables) but here we use tabyl() from janitor and remove the left-most column of value labels before passing to chisq_test().

linelist %>% 
  tabyl(gender, outcome) %>% 
  select(-1) %>% 
  chisq_test()

## # A tibble: 1 x 6
##       n statistic     p    df method          p.signif
## * <dbl>     <dbl> <dbl> <int> <chr>           <chr>   
## 1  5888      3.53 0.473     4 Chi-square test ns

Many many more functions and statistical tests can be run with rstatix functions. See the documentation for rstatix online here or by entering ?rstatix.

18.4 `gtsummary` package

Use gtsummary if you are looking to add the results of a statistical test to a pretty table that was created with this package (as described in the gtsummary section of the Descriptive tables page).

Performing statistical tests of comparison with tbl_summary is done by adding the add_p function to a table and specifying which test to use. It is possible to get p-values corrected for multiple testing by using the add_q function. Run ?tbl_summary for details.

Chi-squared test

Compare the proportions of a categorical variable in two groups. The default statistical test for add_p() when applied to a categorical variable is to perform a chi-squared test of independence with continuity correction, but if any expected call count is below 5 then a Fisher’s exact test is used.

linelist %>% 
  select(gender, outcome) %>%    # keep variables of interest
  tbl_summary(by = outcome) %>%  # produce summary table and specify grouping variable
  add_p()                        # specify what test to perform

## 1323 observations missing `outcome` have been removed. To include these observations, use `forcats::fct_explicit_na()` on `outcome` column before passing to `tbl_summary()`.

Characteristic	Death, N = 2,582¹	Recover, N = 1,983¹	p-value²
gender			>0.9
f	1,227 (50%)	953 (50%)
m	1,228 (50%)	950 (50%)
Unknown	127	80
¹ n (%) ² Pearson's Chi-squared test

T-tests

Compare the difference in means for a continuous variable in two groups. For example, compare the mean age by patient outcome.

linelist %>% 
  select(age_years, outcome) %>%             # keep variables of interest
  tbl_summary(                               # produce summary table
    statistic = age_years ~ "{mean} ({sd})", # specify what statistics to show
    by = outcome) %>%                        # specify the grouping variable
  add_p(age_years ~ "t.test")                # specify what tests to perform

## 1323 observations missing `outcome` have been removed. To include these observations, use `forcats::fct_explicit_na()` on `outcome` column before passing to `tbl_summary()`.

Characteristic	Death, N = 2,582¹	Recover, N = 1,983¹	p-value²
age_years	16 (12)	16 (13)	0.6
Unknown	32	28
¹ Mean (SD) ² Welch Two Sample t-test

Characteristic

Death, N = 2,582¹

Recover, N = 1,983¹

p-value²

age_years

16 (12)

16 (13)

0.6

Unknown

¹ Mean (SD)

² Welch Two Sample t-test

Wilcoxon rank sum test

Compare the distribution of a continuous variable in two groups. The default is to use the Wilcoxon rank sum test and the median (IQR) when comparing two groups. However for non-normally distributed data or comparing multiple groups, the Kruskal-wallis test is more appropriate.

linelist %>% 
  select(age_years, outcome) %>%                       # keep variables of interest
  tbl_summary(                                         # produce summary table
    statistic = age_years ~ "{median} ({p25}, {p75})", # specify what statistic to show (this is default so could remove)
    by = outcome) %>%                                  # specify the grouping variable
  add_p(age_years ~ "wilcox.test")                     # specify what test to perform (default so could leave brackets empty)

## 1323 observations missing `outcome` have been removed. To include these observations, use `forcats::fct_explicit_na()` on `outcome` column before passing to `tbl_summary()`.

Characteristic	Death, N = 2,582¹	Recover, N = 1,983¹	p-value²
age_years	13 (6, 23)	13 (6, 23)	0.8
Unknown	32	28
¹ Median (IQR) ² Wilcoxon rank sum test

Characteristic

Death, N = 2,582¹

Recover, N = 1,983¹

p-value²

age_years

13 (6, 23)

0.8

Unknown

¹ Median (IQR)

² Wilcoxon rank sum test

Kruskal-wallis test

Compare the distribution of a continuous variable in two or more groups, regardless of whether the data is normally distributed.

linelist %>% 
  select(age_years, outcome) %>%                       # keep variables of interest
  tbl_summary(                                         # produce summary table
    statistic = age_years ~ "{median} ({p25}, {p75})", # specify what statistic to show (default, so could remove)
    by = outcome) %>%                                  # specify the grouping variable
  add_p(age_years ~ "kruskal.test")                    # specify what test to perform

## 1323 observations missing `outcome` have been removed. To include these observations, use `forcats::fct_explicit_na()` on `outcome` column before passing to `tbl_summary()`.

Characteristic	Death, N = 2,582¹	Recover, N = 1,983¹	p-value²
age_years	13 (6, 23)	13 (6, 23)	0.8
Unknown	32	28
¹ Median (IQR) ² Kruskal-Wallis rank sum test

Characteristic

Death, N = 2,582¹

Recover, N = 1,983¹

p-value²

age_years

13 (6, 23)

0.8

Unknown

¹ Median (IQR)

² Kruskal-Wallis rank sum test

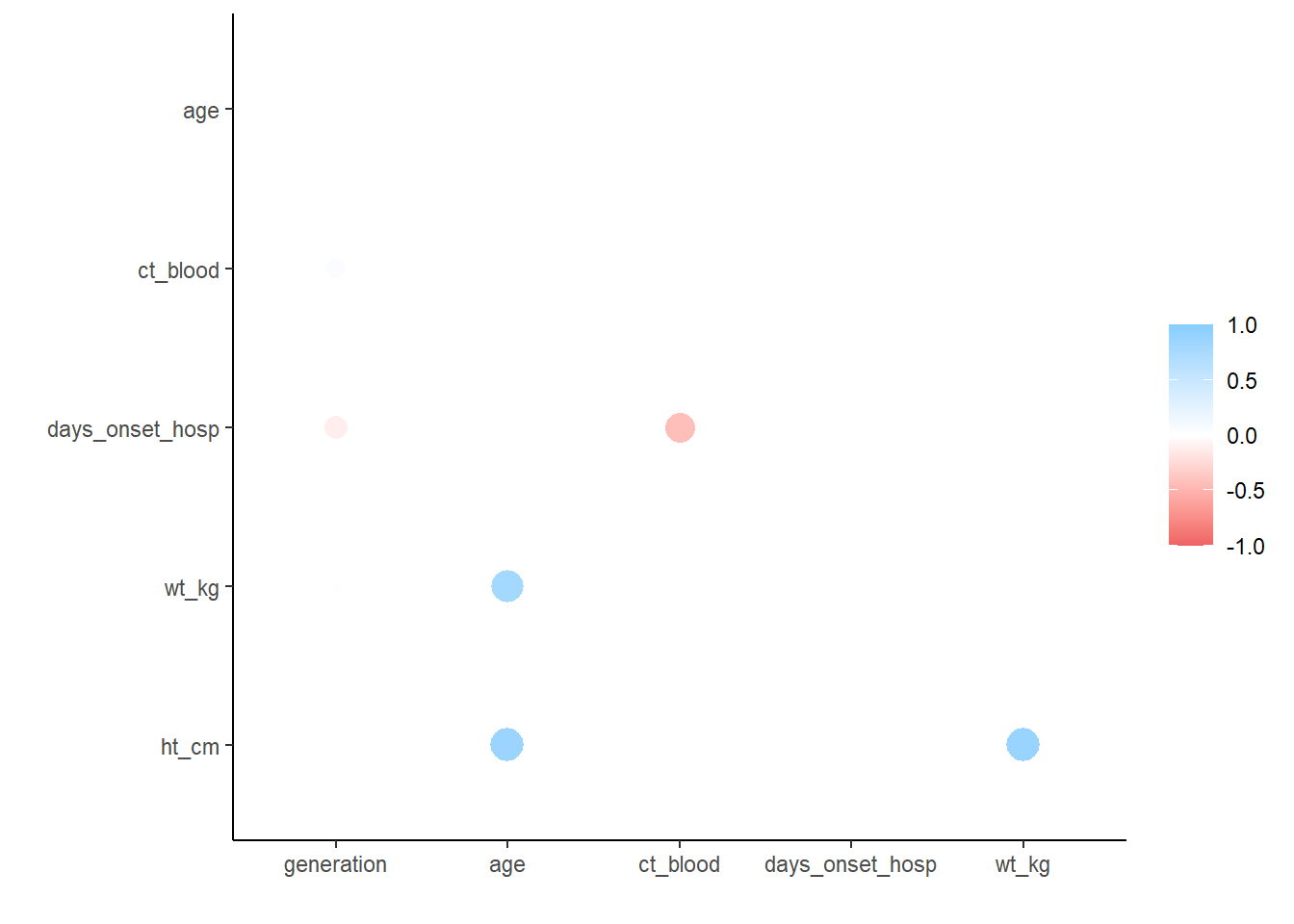
18.5 Correlations

Correlation between numeric variables can be investigated using the tidyverse
corrr package. It allows you to compute correlations using Pearson, Kendall tau or Spearman rho. The package creates a table and also has a function to automatically plot the values.

correlation_tab <- linelist %>% 
  select(generation, age, ct_blood, days_onset_hosp, wt_kg, ht_cm) %>%   # keep numeric variables of interest
  correlate()      # create correlation table (using default pearson)

correlation_tab    # print

## # A tibble: 6 x 7
##   term            generation       age ct_blood days_onset_hosp    wt_kg    ht_cm
##   <chr>                <dbl>     <dbl>    <dbl>           <dbl>    <dbl>    <dbl>
## 1 generation        NA       -0.0222    0.179         -0.288    -0.0302  -0.00942
## 2 age               -0.0222  NA         0.00849       -0.000635  0.833    0.877  
## 3 ct_blood           0.179    0.00849  NA             -0.600    -0.00636  0.0181 
## 4 days_onset_hosp   -0.288   -0.000635 -0.600         NA         0.0153  -0.00953
## 5 wt_kg             -0.0302   0.833    -0.00636        0.0153   NA        0.884  
## 6 ht_cm             -0.00942  0.877     0.0181        -0.00953   0.884   NA

## remove duplicate entries (the table above is mirrored) 
correlation_tab <- correlation_tab %>% 
  shave()

## view correlation table 
correlation_tab

## # A tibble: 6 x 7
##   term            generation       age ct_blood days_onset_hosp  wt_kg ht_cm
##   <chr>                <dbl>     <dbl>    <dbl>           <dbl>  <dbl> <dbl>
## 1 generation        NA       NA        NA              NA       NA        NA
## 2 age               -0.0222  NA        NA              NA       NA        NA
## 3 ct_blood           0.179    0.00849  NA              NA       NA        NA
## 4 days_onset_hosp   -0.288   -0.000635 -0.600          NA       NA        NA
## 5 wt_kg             -0.0302   0.833    -0.00636         0.0153  NA        NA
## 6 ht_cm             -0.00942  0.877     0.0181         -0.00953  0.884    NA

## plot correlations 
rplot(correlation_tab)

18.6 Resources

Much of the information in this page is adapted from these resources and vignettes online:

gtsummary dplyr corrr sthda correlation

17 Descriptive tables

19 Univariate and multivariable regression

18 Simple statistical tests

18.1 Preparation

Load packages

Import data

18.2 base R

T-tests

Shapiro-Wilk test

Wilcoxon rank sum test

Kruskal-Wallis test

Chi-squared test

18.3 rstatix package

Summary statistics

T-test

Shapiro-Wilk test

Wilcoxon rank sum test

Kruskal-Wallis test

Chi-squared test

18.4 gtsummary package

Chi-squared test

T-tests

Wilcoxon rank sum test

Kruskal-wallis test

18.5 Correlations

18.6 Resources

18.4 `gtsummary` package