28 GIS basics
28.1 Overview
Spatial aspects of your data can provide a lot of insights into the situation of the outbreak, and to answer questions such as:
- Where are the current disease hotspots?
- How have the hotspots have changed over time?
- How is the access to health facilities? Are any improvements needed?
The current focus of this GIS page to address the needs of applied epidemiologists in outbreak response. We will explore basic spatial data visualization methods using tmap and ggplot2 packages. We will also walk through some of the basic spatial data management and querying methods with the sf package. Lastly, we will briefly touch upon concepts of spatial statistics such as spatial relationships, spatial autocorrelation, and spatial regression using the spdep package.
28.2 Key terms
Below we introduce some key terminology. For a thorough introduction to GIS and spatial analysis, we suggest that you review one of the longer tutorials or courses listed in the References section.
Geographic Information System (GIS) - A GIS is a framework or environment for gathering, managing, analyzing, and visualizing spatial data.
GIS software
Some popular GIS software allow point-and-click interaction for map development and spatial analysis. These tools comes with advantages such as not needing to learn code and the ease of manually selecting and placing icons and features on a map. Here are two popular ones:
ArcGIS - A commercial GIS software developed by the company ESRI, which is very popular but quite expensive
QGIS - A free open-source GIS software that can do almost anything that ArcGIS can do. You can download QGIS here
Using R as a GIS can seem more intimidating at first because instead of “point-and-click”, it has a “command-line interface” (you must code to acquire the desired outcome). However, this is a major advantage if you need to repetitively produce maps or create an analysis that is reproducible.
Spatial data
The two primary forms of spatial data used in GIS are vector and raster data:
Vector Data - The most common format of spatial data used in GIS, vector data are comprised of geometric features of vertices and paths. Vector spatial data can be further divided into three widely-used types:
Points - A point consists of a coordinate pair (x,y) representing a specific location in a coordinate system. Points are the most basic form of spatial data, and may be used to denote a case (i.e. patient home) or a location (i.e. hospital) on a map.
Lines - A line is composed of two connected points. Lines have a length, and may be used to denote things like roads or rivers.
Polygons - A polygon is composed of at least three line segments connected by points. Polygon features have a length (i.e. the perimeter of the area) as well as an area measurement. Polygons may be used to note an area (i.e. a village) or a structure (i.e. the actual area of a hospital).
Raster Data - An alternative format for spatial data, raster data is a matrix of cells (e.g. pixels) with each cell containing information such as height, temperature, slope, forest cover, etc. These are often aerial photographs, satellite imagery, etc. Rasters can also be used as “base maps” below vector data.
Visualizing spatial data
To visually represent spatial data on a map, GIS software requires you to provide sufficient information about where different features should be, in relation to one another. If you are using vector data, which will be true for most use cases, this information will typically be stored in a shapefile:
Shapefiles - A shapefile is a common data format for storing “vector” spatial data consisting or lines, points, or polygons. A single shapefile is actually a collection of at least three files - .shp, .shx, and .dbf. All of these sub-component files must be present in a given directory (folder) for the shapefile to be readable. These associated files can be compressed into a ZIP folder to be sent via email or download from a website.
The shapefile will contain information about the features themselves, as well as where to locate them on the Earth’s surface. This is important because while the Earth is a globe, maps are typically two-dimensional; choices about how to “flatten” spatial data can have a big impact on the look and interpretation of the resulting map.
Coordinate Reference Systems (CRS) - A CRS is a coordinate-based system used to locate geographical features on the Earth’s surface. It has a few key components:
Coordinate System - There are many many different coordinate systems, so make sure you know which system your coordinates are from. Degrees of latitude/longitude are common, but you could also see UTM coordinates.
Units - Know what the units are for your coordinate system (e.g. decimal degrees, meters)
Datum - A particular modeled version of the Earth. These have been revised over the years, so ensure that your map layers are using the same datum.
Projection - A reference to the mathematical equation that was used to project the truly round earth onto a flat surface (map).
Remember that you can summarise spatial data without using the mapping tools shown below. Sometimes a simple table by geography (e.g. district, country, etc.) is all that is needed!
28.3 Getting started with GIS
There are a couple of key items you will need to have and to think about to make a map. These include:
A dataset – this can be in a spatial data format (such as shapefiles, as noted above) or it may not be in a spatial format (for instance just as a csv).
-
If your dataset is not in a spatial format you will also need a reference dataset. Reference data consists of the spatial representation of the data and the related attributes, which would include material containing the location and address information of specific features.
If you are working with pre-defined geographic boundaries (for example, administrative regions), reference shapefiles are often freely available to download from a government agency or data sharing organization. When in doubt, a good place to start is to Google “[regions] shapefile”
If you have address information, but no latitude and longitude, you may need to use a geocoding engine to get the spatial reference data for your records.
An idea about how you want to present the information in your datasets to your target audience. There are many different types of maps, and it is important to think about which type of map best fits your needs.
Types of maps for visualizing your data
Choropleth map - a type of thematic map where colors, shading, or patterns are used to represent geographic regions in relation to their value of an attribute. For instance a larger value could be indicated by a darker colour than a smaller value. This type of map is particularly useful when visualizing a variable and how it changes across defined regions or geopolitical areas.
Case density heatmap - a type of thematic map where colours are used to represent intensity of a value, however, it does not use defined regions or geopolitical boundaries to group data. This type of map is typically used for showing ‘hot spots’ or areas with a high density or concentration of points.
Dot density map - a thematic map type that uses dots to represent attribute values in your data. This type of map is best used to visualize the scatter of your data and visually scan for clusters.
Proportional symbols map (graduated symbols map) - a thematic map similar to a choropleth map, but instead of using colour to indicate the value of an attribute it uses a symbol (usually a circle) in relation to the value. For instance a larger value could be indicated by a larger symbol than a smaller value. This type of map is best used when you want to visualize the size or quantity of your data across geographic regions.
You can also combine several different types of visualizations to show complex geographic patterns. For example, the cases (dots) in the map below are colored according to their closest health facility (see legend). The large red circles show health facility catchment areas of a certain radius, and the bright red case-dots those that were outside any catchment range:
Note: The primary focus of this GIS page is based on the context of field outbreak response. Therefore the contents of the page will cover the basic spatial data manipulations, visualizations, and analyses.
28.4 Preparation
Load packages
This code chunk shows the loading of packages required for the analyses. In this handbook we emphasize p_load() from pacman, which installs the package if necessary and loads it for use. You can also load installed packages with library() from base R. See the page on [R basics] for more information on R packages.
pacman::p_load(
rio, # to import data
here, # to locate files
tidyverse, # to clean, handle, and plot the data (includes ggplot2 package)
sf, # to manage spatial data using a Simple Feature format
tmap, # to produce simple maps, works for both interactive and static maps
janitor, # to clean column names
OpenStreetMap, # to add OSM basemap in ggplot map
spdep # spatial statistics
) You can see an overview of all the R packages that deal with spatial data at the CRAN “Spatial Task View”.
Sample case data
For demonstration purposes, we will work with a random sample of 1000 cases from the simulated Ebola epidemic linelist dataframe (computationally, working with fewer cases is easier to display in this handbook). If you want to follow along, click to download the “clean” linelist (as .rds file).
Since we are taking a random sample of the cases, your results may look slightly different from what is demonstrated here when you run the codes on your own.
Import data with the import() function from the rio package (it handles many file types like .xlsx, .csv, .rds - see the [Import and export] page for details).
# import clean case linelist
linelist <- import("linelist_cleaned.rds") Next we select a random sample of 1000 rows using sample() from base R.
# generate 1000 random row numbers, from the number of rows in linelist
sample_rows <- sample(nrow(linelist), 1000)
# subset linelist to keep only the sample rows, and all columns
linelist <- linelist[sample_rows,]Now we want to convert this linelist which is class dataframe, to an object of class “sf” (spatial features). Given that the linelist has two columns “lon” and “lat” representing the longitude and latitude of each case’s residence, this will be easy.
We use the package sf (spatial features) and its function st_as_sf() to create the new object we call linelist_sf. This new object looks essentially the same as the linelist, but the columns lon and lat have been designated as coordinate columns, and a coordinate reference system (CRS) has been assigned for when the points are displayed. 4326 identifies our coordinates as based on the World Geodetic System 1984 (WGS84) - which is standard for GPS coordinates.
This is how the original linelist dataframe looks like. In this demonstration, we will only use the column date_onset and geometry (which was constructed from the longitude and latitude fields above and is the last column in the data frame).
Admin boundary shapefiles
Sierra Leone: Admin boundary shapefiles
In advance, we have downloaded all administrative boundaries for Sierra Leone from the Humanitarian Data Exchange (HDX) website here. Alternatively, you can download these and all other example data for this handbook via our R package, as explained in the [Download handbook and data] page.
Now we are going to do the following to save the Admin Level 3 shapefile in R:
- Import the shapefile
- Clean the column names
- Filter rows to keep only areas of interest
To import a shapefile we use the read_sf() function from sf. It is provided the filepath via here(). - in our case the file is within our R project in the “data”, “gis”, and “shp” subfolders, with filename “sle_adm3.shp” (see pages on [Import and export] and [R projects] for more information). You will need to provide your own file path.
Next we use clean_names() from the janitor package to standardize the column names of the shapefile. We also use filter() to keep only the rows with admin2name of “Western Area Urban” or “Western Area Rural”.
# ADM3 level clean
sle_adm3 <- sle_adm3_raw %>%
clean_names() %>% # standardize column names
filter(admin2name %in% c("Western Area Urban", "Western Area Rural")) # filter to keep certain areasBelow you can see the how the shapefile looks after import and cleaning. Scroll to the right to see how there are columns with admin level 0 (country), admin level 1, admin level 2, and finally admin level 3. Each level has a character name and a unique identifier “pcode”. The pcode expands with each increasing admin level e.g. SL (Sierra Leone) -> SL04 (Western) -> SL0410 (Western Area Rural) -> SL040101 (Koya Rural).
Population data
Sierra Leone: Population by ADM3
These data can again be downloaded from HDX (link here) or via our epirhandbook R package as explained [in this page][Download handbook and data]. We use import() to load the .csv file. We also pass the imported file to clean_names() to standardize the column name syntax.
# Population by ADM3
sle_adm3_pop <- import(here("data", "gis", "population", "sle_admpop_adm3_2020.csv")) %>%
clean_names()Here is what the population file looks like. Scroll to the right to see how each jurisdiction has columns with male population, female populaton, total population, and the population break-down in columns by age group.
Health Facilities
Sierra Leone: Health facility data from OpenStreetMap
Again we have downloaded the locations of health facilities from HDX here or via instructions in the [Download handbook and data] page.
We import the facility points shapefile with read_sf(), again clean the column names, and then filter to keep only the points tagged as either “hospital”, “clinic”, or “doctors”.
# OSM health facility shapefile
sle_hf <- sf::read_sf(here("data", "gis", "shp", "sle_hf.shp")) %>%
clean_names() %>%
filter(amenity %in% c("hospital", "clinic", "doctors"))Here is the resulting dataframe - scroll right to see the facility name and geometry coordinates.
28.5 Plotting coordinates
The easiest way to plot X-Y coordinates (longitude/latitude, points), in this case of cases, is to draw them as points directly from the linelist_sf object which we created in the preparation section.
The package tmap offers simple mapping capabilities for both static (“plot” mode) and interactive (“view” mode) with just a few lines of code. The tmap syntax is similar to that of ggplot2, such that commands are added to each other with +. Read more detail in this vignette.
- Set the tmap mode. In this case we will use “plot” mode, which produces static outputs.
tmap_mode("plot") # choose either "view" or "plot"Below, the points are plotted alone.tm_shape() is provided with the linelist_sf objects. We then add points via tm_dots(), specifying the size and color. Because linelist_sf is an sf object, we have already designated the two columns that contain the lat/long coordinates and the coordinate reference system (CRS):
# Just the cases (points)
tm_shape(linelist_sf) + tm_dots(size=0.08, col='blue')
Alone, the points do not tell us much. So we should also map the administrative boundaries:
Again we use tm_shape() (see documentation) but instead of providing the case points shapefile, we provide the administrative boundary shapefile (polygons).
With the bbox = argument (bbox stands for “bounding box”) we can specify the coordinate boundaries. First we show the map display without bbox, and then with it.
# Just the administrative boundaries (polygons)
tm_shape(sle_adm3) + # admin boundaries shapefile
tm_polygons(col = "#F7F7F7")+ # show polygons in light grey
tm_borders(col = "#000000", # show borders with color and line weight
lwd = 2) +
tm_text("admin3name") # column text to display for each polygon
# Same as above, but with zoom from bounding box
tm_shape(sle_adm3,
bbox = c(-13.3, 8.43, # corner
-13.2, 8.5)) + # corner
tm_polygons(col = "#F7F7F7") +
tm_borders(col = "#000000", lwd = 2) +
tm_text("admin3name")
And now both points and polygons together:
# All together
tm_shape(sle_adm3, bbox = c(-13.3, 8.43, -13.2, 8.5)) + #
tm_polygons(col = "#F7F7F7") +
tm_borders(col = "#000000", lwd = 2) +
tm_text("admin3name")+
tm_shape(linelist_sf) +
tm_dots(size=0.08, col='blue', alpha = 0.5) +
tm_layout(title = "Distribution of Ebola cases") # give title to map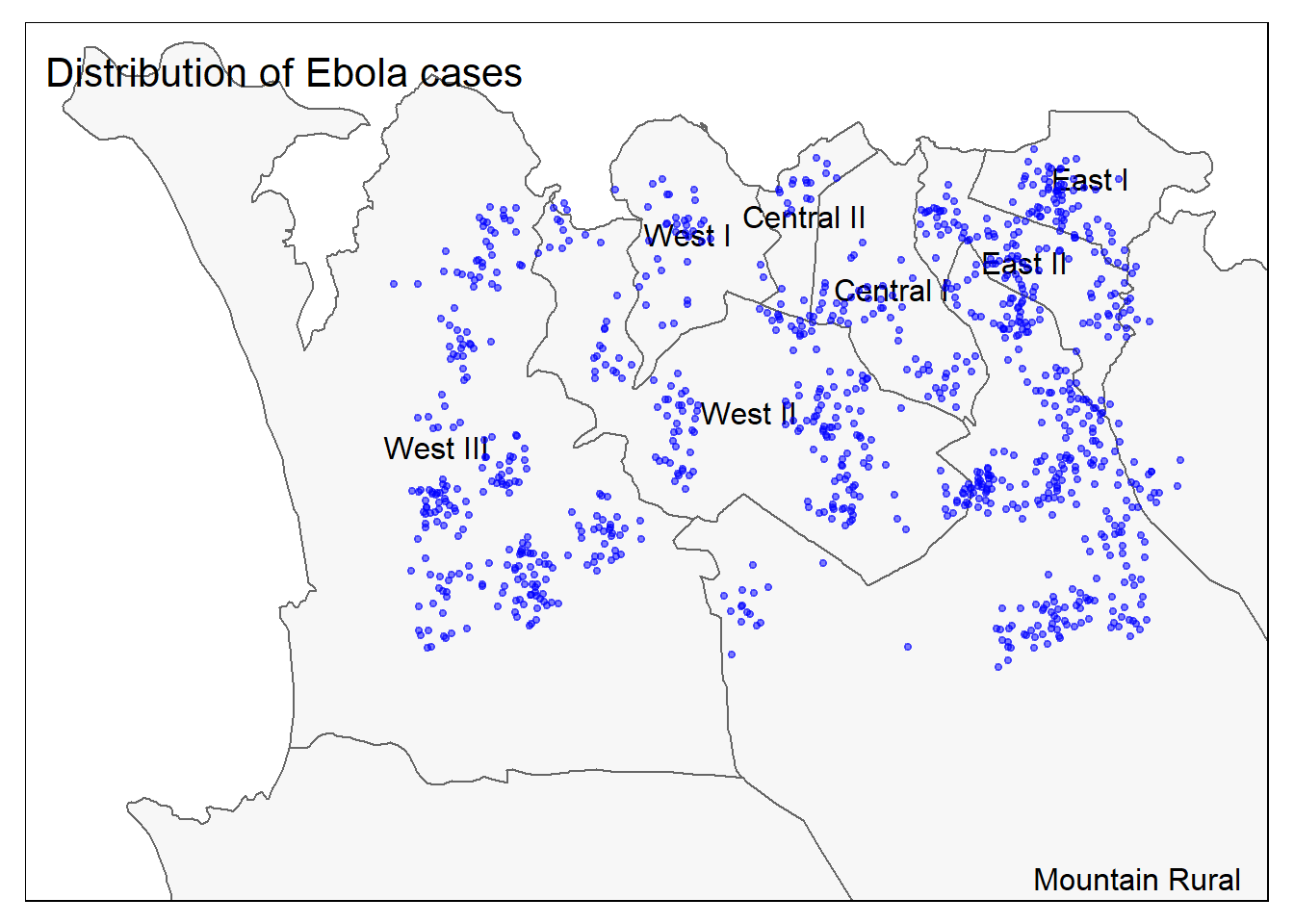
To read a good comparison of mapping options in R, see this blog post.
28.6 Spatial joins
You may be familiar with joining data from one dataset to another one. Several methods are discussed in the Joining data page of this handbook. A spatial join serves a similar purpose but leverages spatial relationships. Instead of relying on common values in columns to correctly match observations, you can utilize their spatial relationships, such as one feature being within another, or the nearest neighbor to another, or within a buffer of a certain radius from another, etc.
The sf package offers various methods for spatial joins. See more documentation about the st_join method and spatial join types in this reference.
Points in polygon
Spatial assign administrative units to cases
Here is an interesting conundrum: the case linelist does not contain any information about the administrative units of the cases. Although it is ideal to collect such information during the initial data collection phase, we can also assign administrative units to individual cases based on their spatial relationships (i.e. point intersects with a polygon).
Below, we will spatially intersect our case locations (points) with the ADM3 boundaries (polygons):
- Begin with the linelist (points)
- Spatial join to the boundaries, setting the type of join at “st_intersects”
- Use
select()to keep only certain of the new administrative boundary columns
linelist_adm <- linelist_sf %>%
# join the administrative boundary file to the linelist, based on spatial intersection
sf::st_join(sle_adm3, join = st_intersects)All the columns from sle_adms have been added to the linelist! Each case now has columns detailing the administrative levels that it falls within. In this example, we only want to keep two of the new columns (admin level 3), so we select() the old column names and just the two additional of interest:
linelist_adm <- linelist_sf %>%
# join the administrative boundary file to the linelist, based on spatial intersection
sf::st_join(sle_adm3, join = st_intersects) %>%
# Keep the old column names and two new admin ones of interest
select(names(linelist_sf), admin3name, admin3pcod)Below, just for display purposes you can see the first ten cases and that their admin level 3 (ADM3) jurisdictions that have been attached, based on where the point spatially intersected with the polygon shapes.
# Now you will see the ADM3 names attached to each case
linelist_adm %>% select(case_id, admin3name, admin3pcod)## Simple feature collection with 1000 features and 3 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: -13.27117 ymin: 8.447961 xmax: -13.20522 ymax: 8.490898
## Geodetic CRS: WGS 84
## First 10 features:
## case_id admin3name admin3pcod geometry
## 2604 43fb82 West II SL040207 POINT (-13.23212 8.467148)
## 5024 5f8f6c West II SL040207 POINT (-13.23171 8.466273)
## 639 de3b80 West II SL040207 POINT (-13.23677 8.475543)
## 5253 846579 East I SL040203 POINT (-13.20988 8.482548)
## 5667 67cb00 West III SL040208 POINT (-13.25547 8.458662)
## 4367 adbb4a West II SL040207 POINT (-13.22997 8.464757)
## 3904 aae7de West III SL040208 POINT (-13.26751 8.467827)
## 1578 948d51 Mountain Rural SL040102 POINT (-13.20994 8.452937)
## 3489 24c64b West III SL040208 POINT (-13.26509 8.451107)
## 360 3ac4d6 Central II SL040202 POINT (-13.23655 8.488145)Now we can describe our cases by administrative unit - something we were not able to do before the spatial join!
# Make new dataframe containing counts of cases by administrative unit
case_adm3 <- linelist_adm %>% # begin with linelist with new admin cols
as_tibble() %>% # convert to tibble for better display
group_by(admin3pcod, admin3name) %>% # group by admin unit, both by name and pcode
summarise(cases = n()) %>% # summarize and count rows
arrange(desc(cases)) %>% # arrange in descending order
filter(!is.na(admin3name))
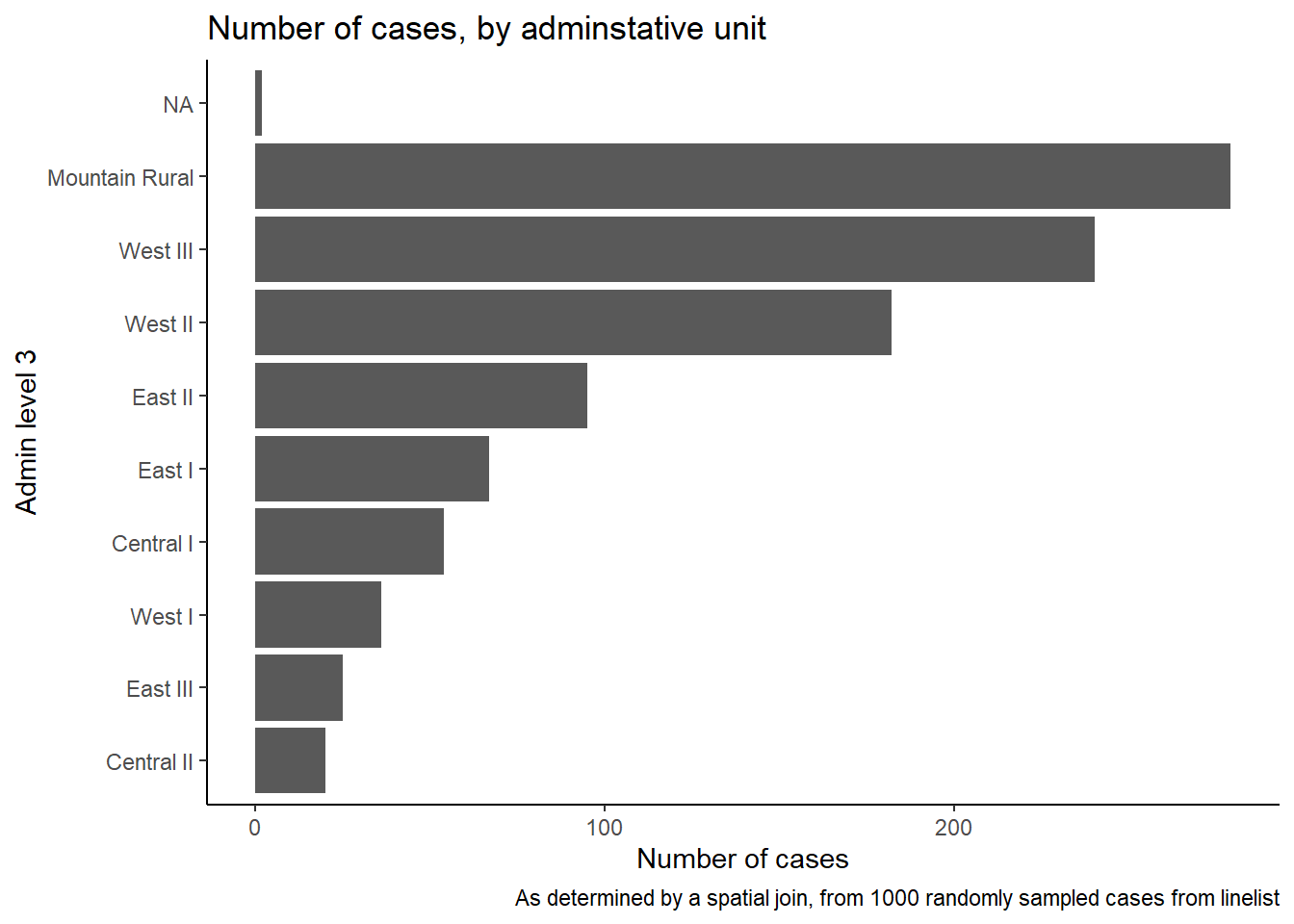
case_adm3## # A tibble: 9 x 3
## # Groups: admin3pcod [9]
## admin3pcod admin3name cases
## <chr> <chr> <int>
## 1 SL040102 Mountain Rural 279
## 2 SL040208 West III 240
## 3 SL040207 West II 182
## 4 SL040204 East II 95
## 5 SL040203 East I 67
## 6 SL040201 Central I 54
## 7 SL040206 West I 36
## 8 SL040205 East III 25
## 9 SL040202 Central II 20We can also create a bar plot of case counts by administrative unit.
In this example, we begin the ggplot() with the linelist_adm, so that we can apply factor functions like fct_infreq() which orders the bars by frequency (see page on Factors for tips).
ggplot(
data = linelist_adm, # begin with linelist containing admin unit info
mapping = aes(
x = fct_rev(fct_infreq(admin3name))))+ # x-axis is admin units, ordered by frequency (reversed)
geom_bar()+ # create bars, height is number of rows
coord_flip()+ # flip X and Y axes for easier reading of adm units
theme_classic()+ # simplify background
labs( # titles and labels
x = "Admin level 3",
y = "Number of cases",
title = "Number of cases, by adminstative unit",
caption = "As determined by a spatial join, from 1000 randomly sampled cases from linelist"
)
Nearest neighbor
Finding the nearest health facility / catchment area
It might be useful to know where the health facilities are located in relation to the disease hot spots.
We can use the st_nearest_feature join method from the st_join() function (sf package) to visualize the closest health facility to individual cases.
- We begin with the shapefile linelist
linelist_sf
- We spatially join with
sle_hf, which is the locations of health facilities and clinics (points)
# Closest health facility to each case
linelist_sf_hf <- linelist_sf %>% # begin with linelist shapefile
st_join(sle_hf, join = st_nearest_feature) %>% # data from nearest clinic joined to case data
select(case_id, osm_id, name, amenity) %>% # keep columns of interest, including id, name, type, and geometry of healthcare facility
rename("nearest_clinic" = "name") # re-name for clarityWe can see below (first 50 rows) that the each case now has data on the nearest clinic/hospital
We can see that “Den Clinic” is the closest health facility for about ~30% of the cases.
# Count cases by health facility
hf_catchment <- linelist_sf_hf %>% # begin with linelist including nearest clinic data
as.data.frame() %>% # convert from shapefile to dataframe
count(nearest_clinic, # count rows by "name" (of clinic)
name = "case_n") %>% # assign new counts column as "case_n"
arrange(desc(case_n)) # arrange in descending order
hf_catchment # print to console## nearest_clinic case_n
## 1 Den Clinic 368
## 2 Shriners Hospitals for Children 320
## 3 GINER HALL COMMUNITY HOSPITAL 174
## 4 panasonic 49
## 5 Princess Christian Maternity Hospital 38
## 6 ARAB EGYPT CLINIC 23
## 7 <NA> 17
## 8 MABELL HEALTH CENTER 11To visualize the results, we can use tmap - this time interactive mode for easier viewing
tmap_mode("view") # set tmap mode to interactive
# plot the cases and clinic points
tm_shape(linelist_sf_hf) + # plot cases
tm_dots(size=0.08, # cases colored by nearest clinic
col='nearest_clinic') +
tm_shape(sle_hf) + # plot clinic facilities in large black dots
tm_dots(size=0.3, col='black', alpha = 0.4) +
tm_text("name") + # overlay with name of facility
tm_view(set.view = c(-13.2284, 8.4699, 13), # adjust zoom (center coords, zoom)
set.zoom.limits = c(13,14))+
tm_layout(title = "Cases, colored by nearest clinic")Buffers
We can also explore how many cases are located within 2.5km (~30 mins) walking distance from the closest health facility.
Note: For more accurate distance calculations, it is better to re-project your sf object to the respective local map projection system such as UTM (Earth projected onto a planar surface). In this example, for simplicity we will stick to the World Geodetic System (WGS84) Geograhpic coordinate system (Earth represented in a spherical / round surface, therefore the units are in decimal degrees). We will use a general conversion of: 1 decimal degree = ~111km.
See more information about map projections and coordinate systems at this esri article. This blog talks about different types of map projection and how one can choose a suitable projection depending on the area of interest and the context of your map / analysis.
First, create a circular buffer with a radius of ~2.5km around each health facility. This is done with the function st_buffer() from tmap. Because the unit of the map is in lat/long decimal degrees, that is how “0.02” is interpreted. If your map coordinate system is in meters, the number must be provided in meters.
sle_hf_2k <- sle_hf %>%
st_buffer(dist=0.02) # decimal degrees translating to approximately 2.5km Below we plot the buffer zones themselves, with the :
tmap_mode("plot")
# Create circular buffers
tm_shape(sle_hf_2k) +
tm_borders(col = "black", lwd = 2)+
tm_shape(sle_hf) + # plot clinic facilities in large red dots
tm_dots(size=0.3, col='black') 
**Second, we intersect these buffers with the cases (points) using st_join() and the join type of st_intersects*. That is, the data from the buffers are joined to the points that they intersect with.
# Intersect the cases with the buffers
linelist_sf_hf_2k <- linelist_sf_hf %>%
st_join(sle_hf_2k, join = st_intersects, left = TRUE) %>%
filter(osm_id.x==osm_id.y | is.na(osm_id.y)) %>%
select(case_id, osm_id.x, nearest_clinic, amenity.x, osm_id.y)Now we can count the results: nrow(linelist_sf_hf_2k[is.na(linelist_sf_hf_2k$osm_id.y),]) out of 1000 cases did not intersect with any buffer (that value is missing), and so live more than 30 mins walk from the nearest health facility.
# Cases which did not get intersected with any of the health facility buffers
linelist_sf_hf_2k %>%
filter(is.na(osm_id.y)) %>%
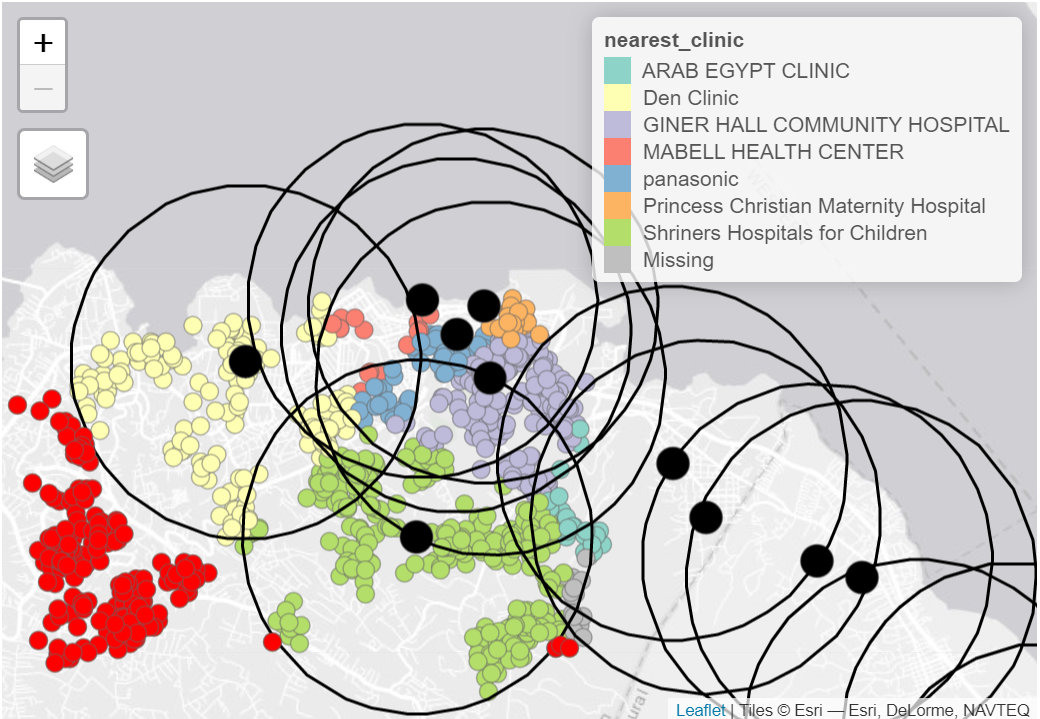
nrow()## [1] 1000We can visualize the results such that cases that did not intersect with any buffer appear in red.
tmap_mode("view")
# First display the cases in points
tm_shape(linelist_sf_hf) +
tm_dots(size=0.08, col='nearest_clinic') +
# plot clinic facilities in large black dots
tm_shape(sle_hf) +
tm_dots(size=0.3, col='black')+
# Then overlay the health facility buffers in polylines
tm_shape(sle_hf_2k) +
tm_borders(col = "black", lwd = 2) +
# Highlight cases that are not part of any health facility buffers
# in red dots
tm_shape(linelist_sf_hf_2k %>% filter(is.na(osm_id.y))) +
tm_dots(size=0.1, col='red') +
tm_view(set.view = c(-13.2284,8.4699, 13), set.zoom.limits = c(13,14))+
# add title
tm_layout(title = "Cases by clinic catchment area")Other spatial joins
Alternative values for argument join include (from the documentation)
- st_contains_properly
- st_contains
- st_covered_by
- st_covers
- st_crosses
- st_disjoint
- st_equals_exact
- st_equals
- st_is_within_distance
- st_nearest_feature
- st_overlaps
- st_touches
- st_within
28.7 Choropleth maps
Choropleth maps can be useful to visualize your data by pre-defined area, usually administrative unit or health area. In outbreak response this can help to target resource allocation for specific areas with high incidence rates, for example.
Now that we have the administrative unit names assigned to all cases (see section on spatial joins, above), we can start mapping the case counts by area (choropleth maps).
Since we also have population data by ADM3, we can add this information to the case_adm3 table created previously.
We begin with the dataframe created in the previous step case_adm3, which is a summary table of each administrative unit and its number of cases.
- The population data
sle_adm3_popare joined using aleft_join()from dplyr on the basis of common values across columnadmin3pcodin thecase_adm3dataframe, and columnadm_pcodein thesle_adm3_popdataframe. See page on Joining data).
-
select()is applied to the new dataframe, to keep only the useful columns -totalis total population
- Cases per 10,000 populaton is calculated as a new column with
mutate()
# Add population data and calculate cases per 10K population
case_adm3 <- case_adm3 %>%
left_join(sle_adm3_pop, # add columns from pop dataset
by = c("admin3pcod" = "adm3_pcode")) %>% # join based on common values across these two columns
select(names(case_adm3), total) %>% # keep only important columns, including total population
mutate(case_10kpop = round(cases/total * 10000, 3)) # make new column with case rate per 10000, rounded to 3 decimals
case_adm3 # print to console for viewing## # A tibble: 9 x 5
## # Groups: admin3pcod [9]
## admin3pcod admin3name cases total case_10kpop
## <chr> <chr> <int> <int> <dbl>
## 1 SL040102 Mountain Rural 279 33993 82.1
## 2 SL040208 West III 240 210252 11.4
## 3 SL040207 West II 182 145109 12.5
## 4 SL040204 East II 95 99821 9.52
## 5 SL040203 East I 67 68284 9.81
## 6 SL040201 Central I 54 69683 7.75
## 7 SL040206 West I 36 60186 5.98
## 8 SL040205 East III 25 500134 0.5
## 9 SL040202 Central II 20 23874 8.38Join this table with the ADM3 polygons shapefile for mapping
case_adm3_sf <- case_adm3 %>% # begin with cases & rate by admin unit
left_join(sle_adm3, by="admin3pcod") %>% # join to shapefile data by common column
select(objectid, admin3pcod, # keep only certain columns of interest
admin3name = admin3name.x, # clean name of one column
admin2name, admin1name,
cases, total, case_10kpop,
geometry) %>% # keep geometry so polygons can be plotted
st_as_sf() # convert to shapefileMapping the results
# tmap mode
tmap_mode("plot") # view static map
# plot polygons
tm_shape(case_adm3_sf) +
tm_polygons("cases") + # color by number of cases column
tm_text("admin3name") # name display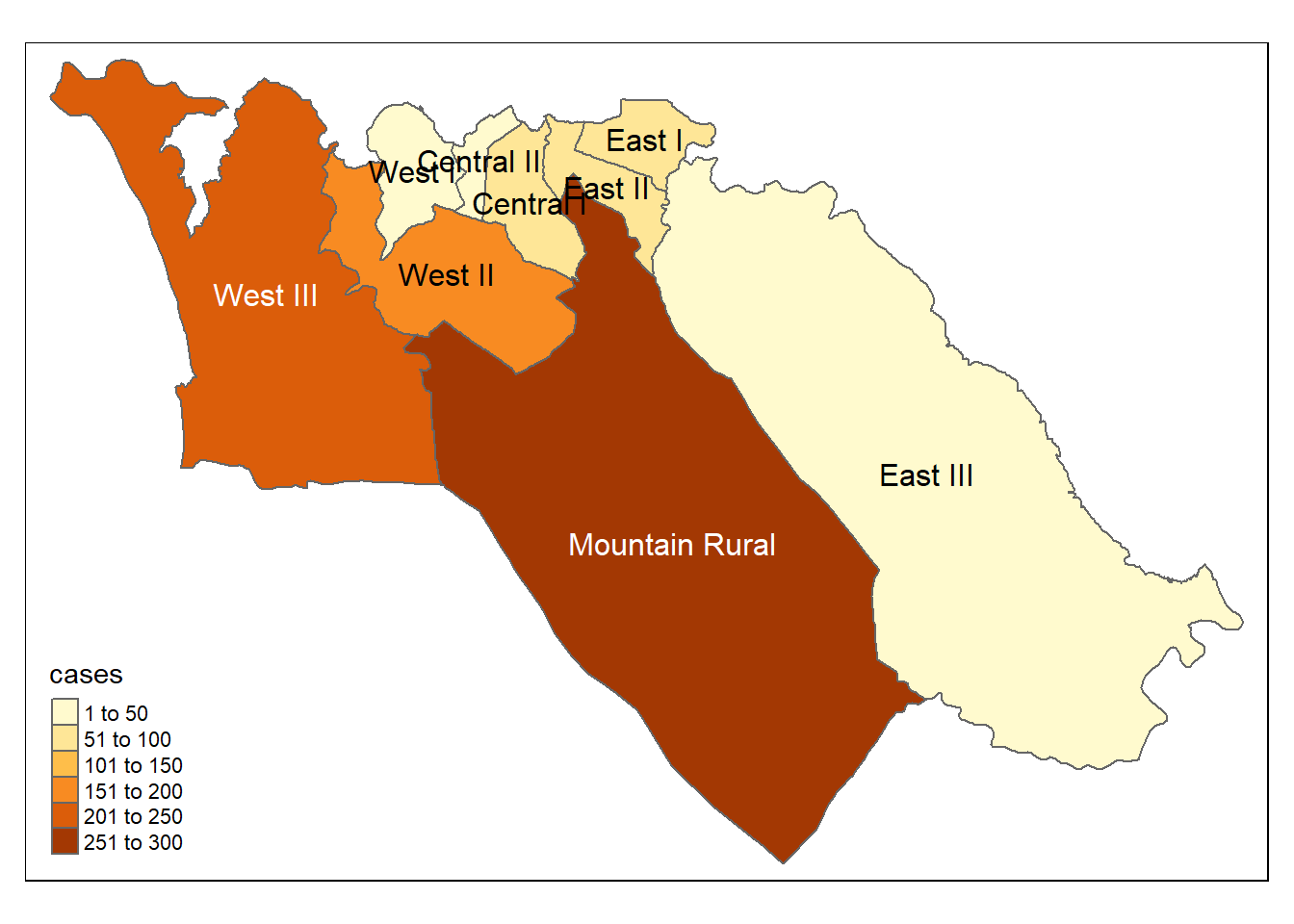
We can also map the incidence rates
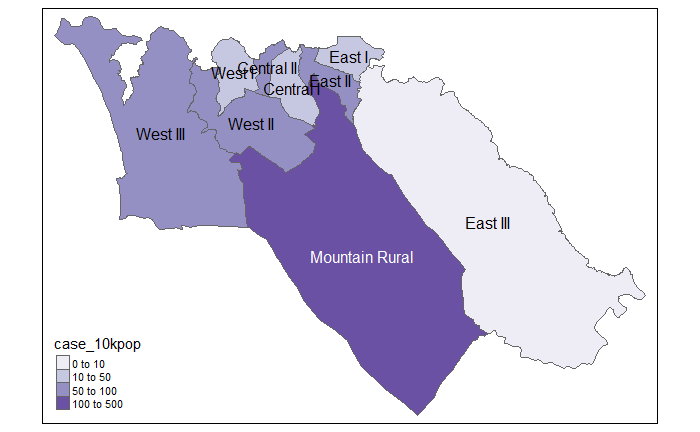
# Cases per 10K population
tmap_mode("plot") # static viewing mode
# plot
tm_shape(case_adm3_sf) + # plot polygons
tm_polygons("case_10kpop", # color by column containing case rate
breaks=c(0, 10, 50, 100), # define break points for colors
palette = "Purples" # use a purple color palette
) +
tm_text("admin3name") # display text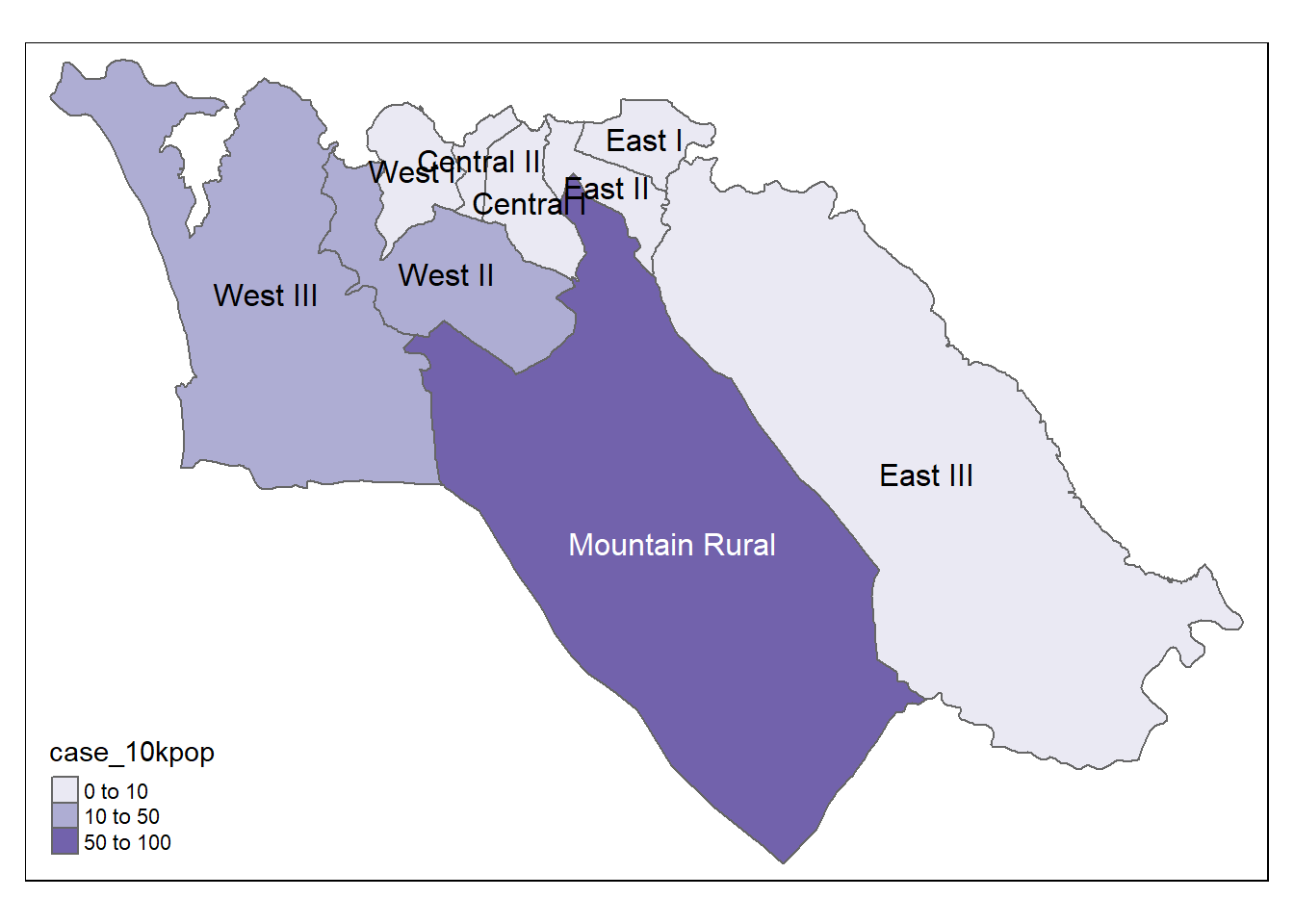
28.8 Mapping with ggplot2
If you are already familiar with using ggplot2, you can use that package instead to create static maps of your data. The geom_sf() function will draw different objects based on which features (points, lines, or polygons) are in your data. For example, you can use geom_sf() in a ggplot() using sf data with polygon geometry to create a choropleth map.
To illustrate how this works, we can start with the ADM3 polygons shapefile that we used earlier. Recall that these are Admin Level 3 regions in Sierra Leone:
sle_adm3## Simple feature collection with 12 features and 19 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: -13.29894 ymin: 8.094272 xmax: -12.91333 ymax: 8.499809
## Geodetic CRS: WGS 84
## # A tibble: 12 x 20
## objectid admin3name admin3pcod admin3ref_n admin2name admin2pcod admin1name admin1pcod admin0name admin0pcod date
## * <dbl> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <date>
## 1 155 Koya Rural SL040101 Koya Rural Western Are~ SL0401 Western SL04 Sierra Le~ SL 2016-08-01
## 2 156 Mountain Rural SL040102 Mountain Ru~ Western Are~ SL0401 Western SL04 Sierra Le~ SL 2016-08-01
## 3 157 Waterloo Rural SL040103 Waterloo Ru~ Western Are~ SL0401 Western SL04 Sierra Le~ SL 2016-08-01
## 4 158 York Rural SL040104 York Rural Western Are~ SL0401 Western SL04 Sierra Le~ SL 2016-08-01
## 5 159 Central I SL040201 Central I Western Are~ SL0402 Western SL04 Sierra Le~ SL 2016-08-01
## 6 160 East I SL040203 East I Western Are~ SL0402 Western SL04 Sierra Le~ SL 2016-08-01
## 7 161 East II SL040204 East II Western Are~ SL0402 Western SL04 Sierra Le~ SL 2016-08-01
## 8 162 Central II SL040202 Central II Western Are~ SL0402 Western SL04 Sierra Le~ SL 2016-08-01
## 9 163 West III SL040208 West III Western Are~ SL0402 Western SL04 Sierra Le~ SL 2016-08-01
## 10 164 West I SL040206 West I Western Are~ SL0402 Western SL04 Sierra Le~ SL 2016-08-01
## 11 165 West II SL040207 West II Western Are~ SL0402 Western SL04 Sierra Le~ SL 2016-08-01
## 12 167 East III SL040205 East III Western Are~ SL0402 Western SL04 Sierra Le~ SL 2016-08-01
## # ... with 9 more variables: valid_on <date>, valid_to <date>, shape_leng <dbl>, shape_area <dbl>, rowcacode0 <chr>,
## # rowcacode1 <chr>, rowcacode2 <chr>, rowcacode3 <chr>, geometry <MULTIPOLYGON [arc_degree]>We can use the left_join() function from dplyr to add the data we would like to map to the shapefile object. In this case, we are going to use the case_adm3 data frame that we created earlier to summarize case counts by administrative region; however, we can use this same approach to map any data stored in a data frame.
sle_adm3_dat <- sle_adm3 %>%
inner_join(case_adm3, by = "admin3pcod") # inner join = retain only if in both data objects
select(sle_adm3_dat, admin3name.x, cases) # print selected variables to console## Simple feature collection with 9 features and 2 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: -13.29894 ymin: 8.384533 xmax: -13.12612 ymax: 8.499809
## Geodetic CRS: WGS 84
## # A tibble: 9 x 3
## admin3name.x cases geometry
## <chr> <int> <MULTIPOLYGON [arc_degree]>
## 1 Mountain Rural 279 (((-13.21496 8.474341, -13.21479 8.474289, -13.21465 8.474296, -13.21455 8.474298, -...
## 2 Central I 54 (((-13.22646 8.489716, -13.22648 8.48955, -13.22644 8.489513, -13.22663 8.489229, -1...
## 3 East I 67 (((-13.2129 8.494033, -13.21076 8.494026, -13.21013 8.494041, -13.2096 8.494025, -13...
## 4 East II 95 (((-13.22653 8.491883, -13.22647 8.491853, -13.22642 8.49186, -13.22633 8.491814, -1...
## 5 Central II 20 (((-13.23154 8.491768, -13.23141 8.491566, -13.23144 8.49146, -13.23131 8.491294, -1...
## 6 West III 240 (((-13.28529 8.497354, -13.28456 8.496497, -13.28403 8.49621, -13.28338 8.496086, -1...
## 7 West I 36 (((-13.24677 8.493453, -13.24669 8.493285, -13.2464 8.493132, -13.24627 8.493131, -1...
## 8 West II 182 (((-13.25698 8.485518, -13.25685 8.485501, -13.25668 8.485505, -13.25657 8.485504, -...
## 9 East III 25 (((-13.20465 8.485758, -13.20461 8.485698, -13.20449 8.485757, -13.20431 8.485577, -...To make a column chart of case counts by region, using ggplot2, we could then call geom_col() as follows:
ggplot(data=sle_adm3_dat) +
geom_col(aes(x=fct_reorder(admin3name.x, cases, .desc=T), # reorder x axis by descending 'cases'
y=cases)) + # y axis is number of cases by region
theme_bw() +
labs( # set figure text
title="Number of cases, by administrative unit",
x="Admin level 3",
y="Number of cases"
) +
guides(x=guide_axis(angle=45)) # angle x-axis labels 45 degrees to fit better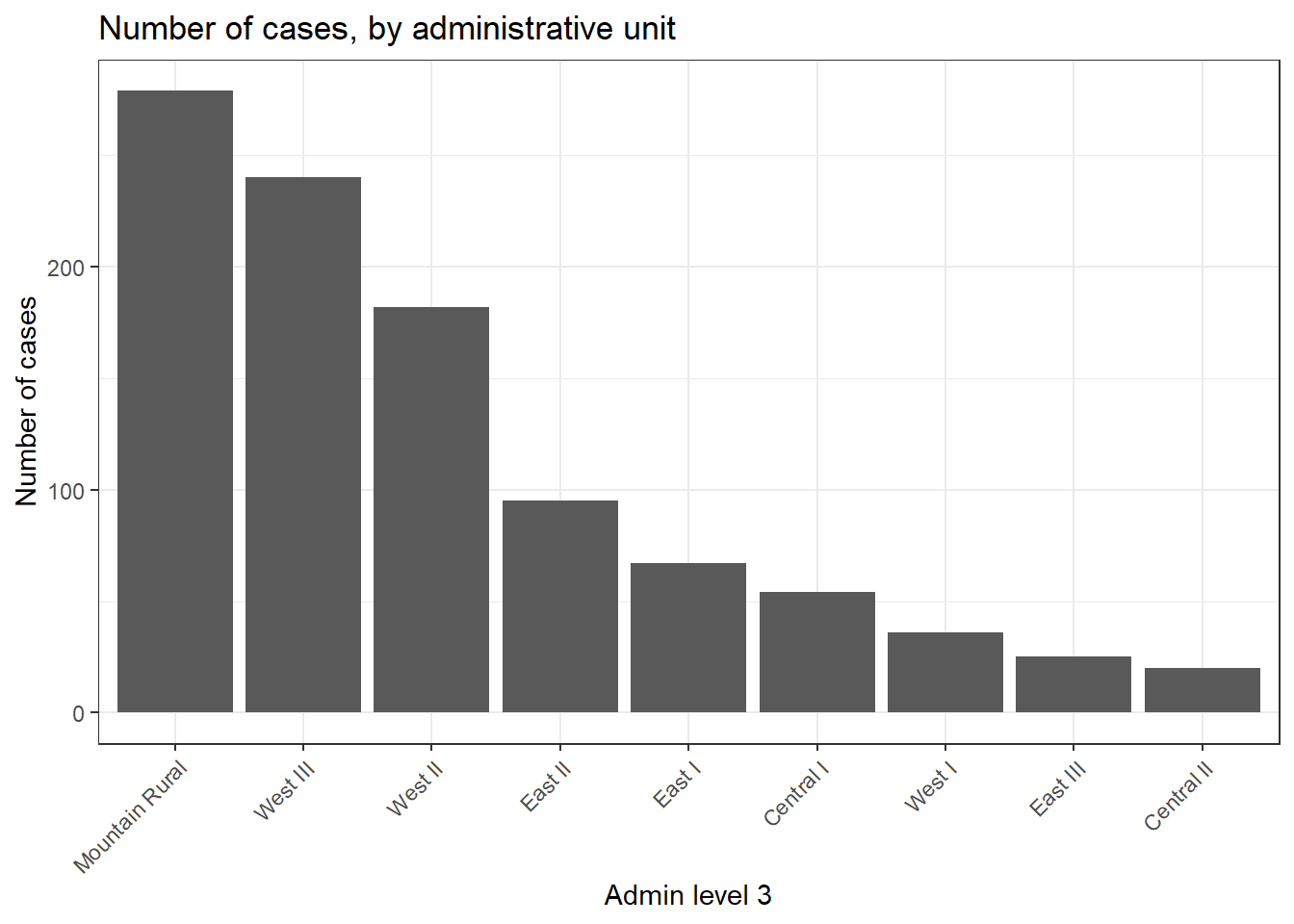
If we want to use ggplot2 to instead make a choropleth map of case counts, we can use similar syntax to call the geom_sf() function:
ggplot(data=sle_adm3_dat) +
geom_sf(aes(fill=cases)) # set fill to vary by case count variable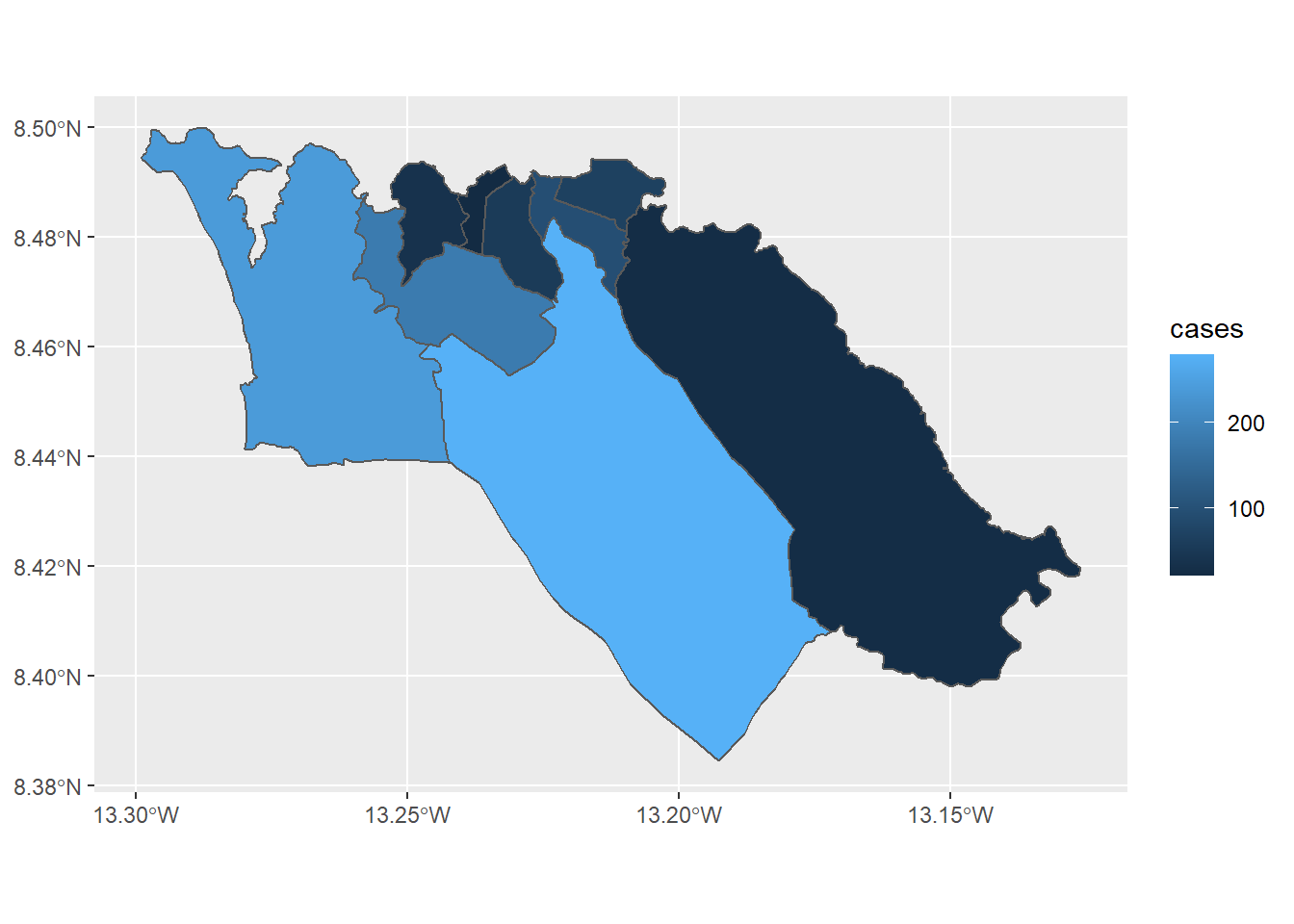
We can then customize the appearance of our map using grammar that is consistent across ggplot2, for example:
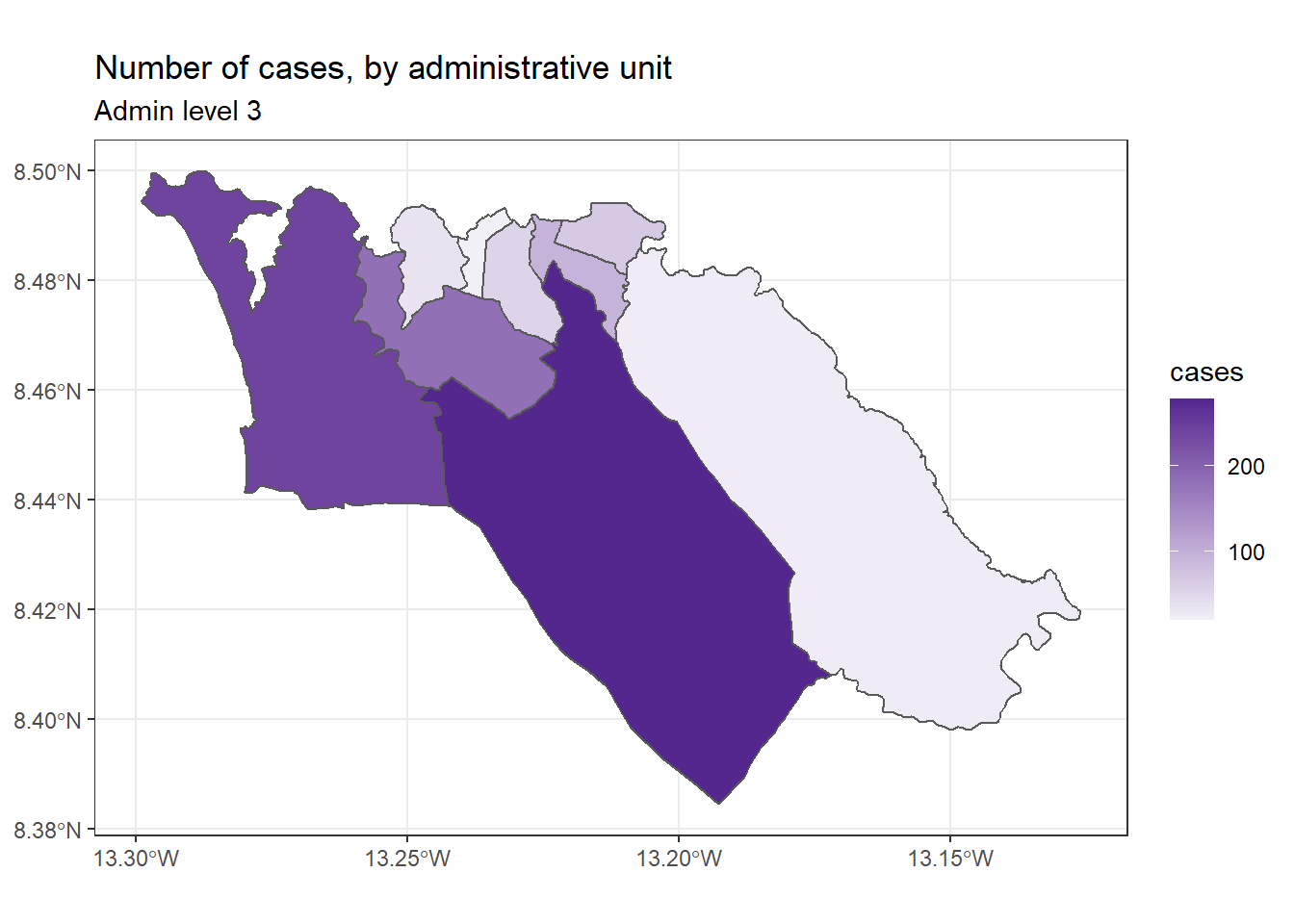
ggplot(data=sle_adm3_dat) +
geom_sf(aes(fill=cases)) +
scale_fill_continuous(high="#54278f", low="#f2f0f7") + # change color gradient
theme_bw() +
labs(title = "Number of cases, by administrative unit", # set figure text
subtitle = "Admin level 3"
)
For R users who are comfortable working with ggplot2, geom_sf() offers a simple and direct implementation that is suitable for basic map visualizations. To learn more, read the geom_sf() vignette or the ggplot2 book.
28.9 Basemaps
OpenStreetMap
Below we describe how to achieve a basemap for a ggplot2 map using OpenStreetMap features. Alternative methods include using ggmap which requires free registration with Google (details).
OpenStreetMap is a collaborative project to create a free editable map of the world. The underlying geolocation data (e.g. locations of cities, roads, natural features, airports, schools, hospitals, roads etc) are considered the primary output of the project.
First we load the OpenStreetMap package, from which we will get our basemap.
Then, we create the object map, which we define using the function openmap() from OpenStreetMap package (documentation). We provide the following:
-
upperLeftandlowerRightTwo coordinate pairs specifying the limits of the basemap tile- In this case we’ve put in the max and min from the linelist rows, so the map will respond dynamically to the data
- In this case we’ve put in the max and min from the linelist rows, so the map will respond dynamically to the data
-
zoom =(if null it is determined automatically)
-
type =which type of basemap - we have listed several possibilities here and the code is currently using the first one ([1]) “osm”
-
mergeTiles =we chose TRUE so the basetiles are all merged into one
# load package
pacman::p_load(OpenStreetMap)
# Fit basemap by range of lat/long coordinates. Choose tile type
map <- openmap(
upperLeft = c(max(linelist$lat, na.rm=T), max(linelist$lon, na.rm=T)), # limits of basemap tile
lowerRight = c(min(linelist$lat, na.rm=T), min(linelist$lon, na.rm=T)),
zoom = NULL,
type = c("osm", "stamen-toner", "stamen-terrain", "stamen-watercolor", "esri","esri-topo")[1])If we plot this basemap right now, using autoplot.OpenStreetMap() from OpenStreetMap package, you see that the units on the axes are not latitude/longitude coordinates. It is using a different coordinate system. To correctly display the case residences (which are stored in lat/long), this must be changed.
autoplot.OpenStreetMap(map)
Thus, we want to convert the map to latitude/longitude with the openproj() function from OpenStreetMap package. We provide the basemap map and also provide the Coordinate Reference System (CRS) we want. We do this by providing the “proj.4” character string for the WGS 1984 projection, but you can provide the CRS in other ways as well. (see this page to better understand what a proj.4 string is)
# Projection WGS84
map_latlon <- openproj(map, projection = "+proj=longlat +ellps=WGS84 +datum=WGS84 +no_defs")Now when we create the plot we see that along the axes are latitude and longitude coordinate. The coordinate system has been converted. Now our cases will plot correctly if overlaid!
# Plot map. Must use "autoplot" in order to work with ggplot
autoplot.OpenStreetMap(map_latlon)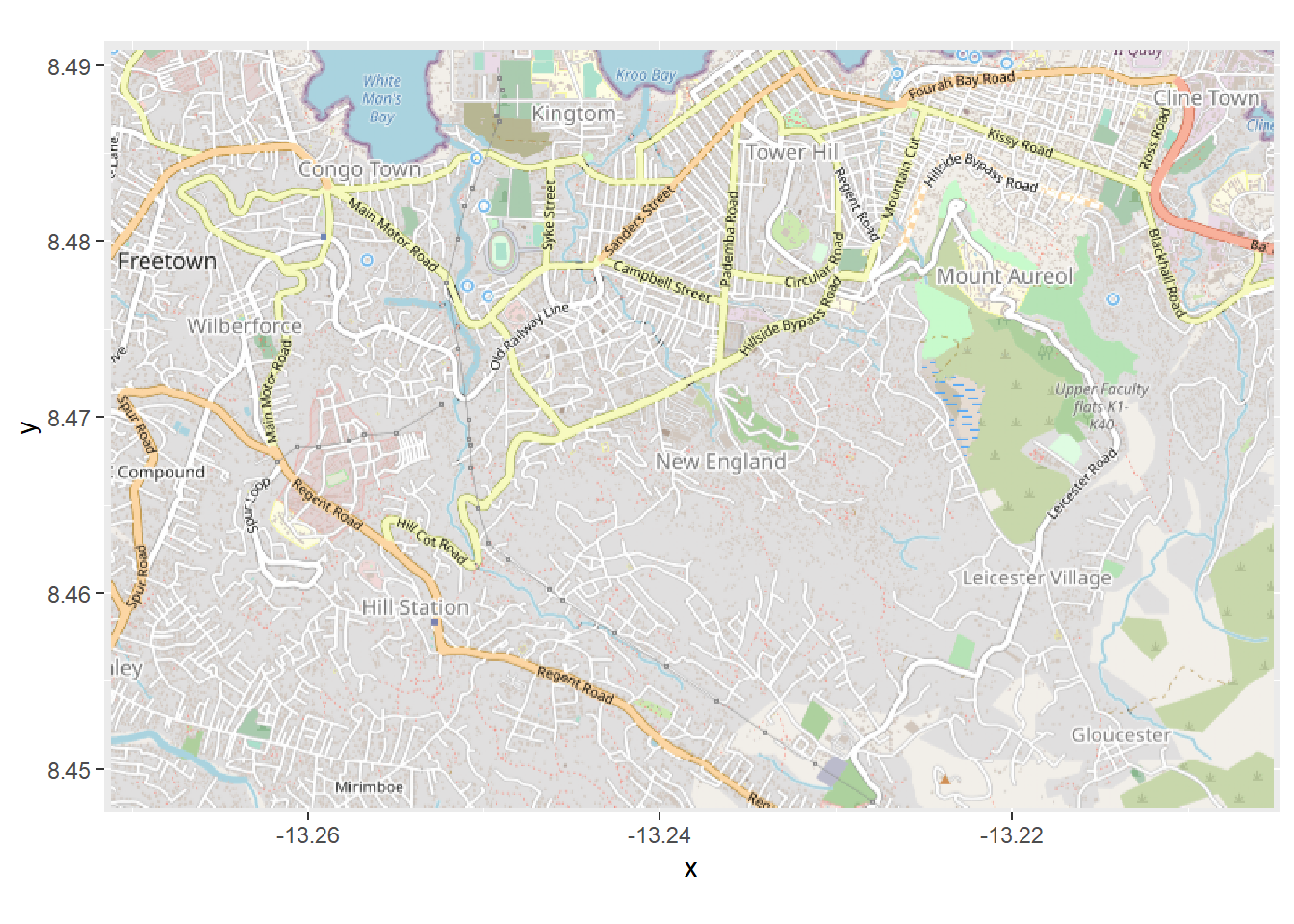
28.10 Contoured density heatmaps
Below we describe how to achieve a contoured density heatmap of cases, over a basemap, beginning with a linelist (one row per case).
- Create basemap tile from OpenStreetMap, as described above
- Plot the cases from
linelistusing the latitude and longitude columns
- Convert the points to a density heatmap with
stat_density_2d()from ggplot2,
When we have a basemap with lat/long coordinates, we can plot our cases on top using the lat/long coordinates of their residence.
Building on the function autoplot.OpenStreetMap() to create the basemap, ggplot2 functions will easily add on top, as shown with geom_point() below:
# Plot map. Must be autoplotted to work with ggplot
autoplot.OpenStreetMap(map_latlon)+ # begin with the basemap
geom_point( # add xy points from linelist lon and lat columns
data = linelist,
aes(x = lon, y = lat),
size = 1,
alpha = 0.5,
show.legend = FALSE) + # drop legend entirely
labs(x = "Longitude", # titles & labels
y = "Latitude",
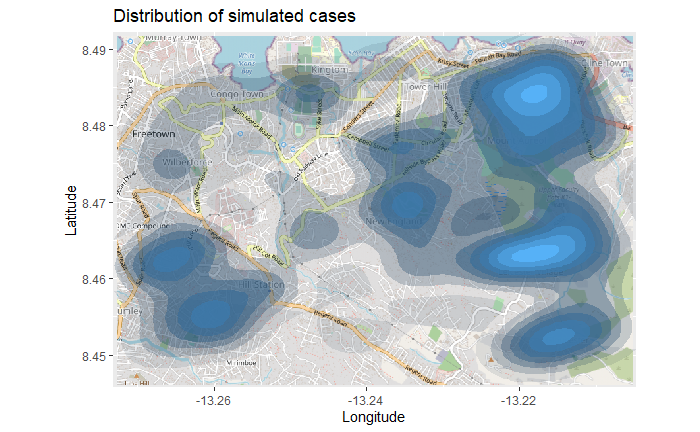
title = "Cumulative cases")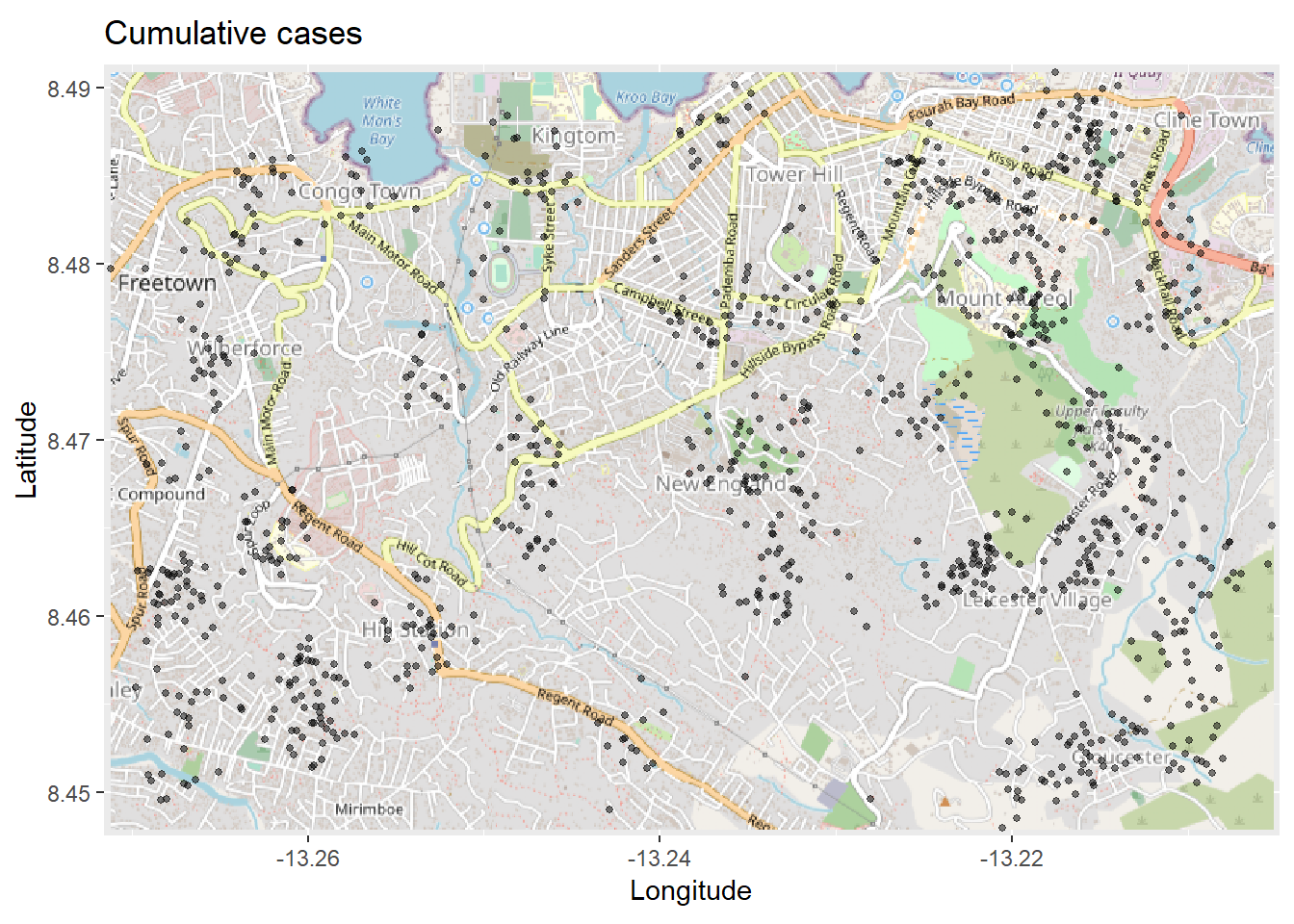
The map above might be difficult to interpret, especially with the points overlapping. So you can instead plot a 2d density map using the ggplot2 function stat_density_2d(). You are still using the linelist lat/lon coordinates, but a 2D kernel density estimation is performed and the results are displayed with contour lines - like a topographical map. Read the full documentation here.
# begin with the basemap
autoplot.OpenStreetMap(map_latlon)+
# add the density plot
ggplot2::stat_density_2d(
data = linelist,
aes(
x = lon,
y = lat,
fill = ..level..,
alpha = ..level..),
bins = 10,
geom = "polygon",
contour_var = "count",
show.legend = F) +
# specify color scale
scale_fill_gradient(low = "black", high = "red")+
# labels
labs(x = "Longitude",
y = "Latitude",
title = "Distribution of cumulative cases")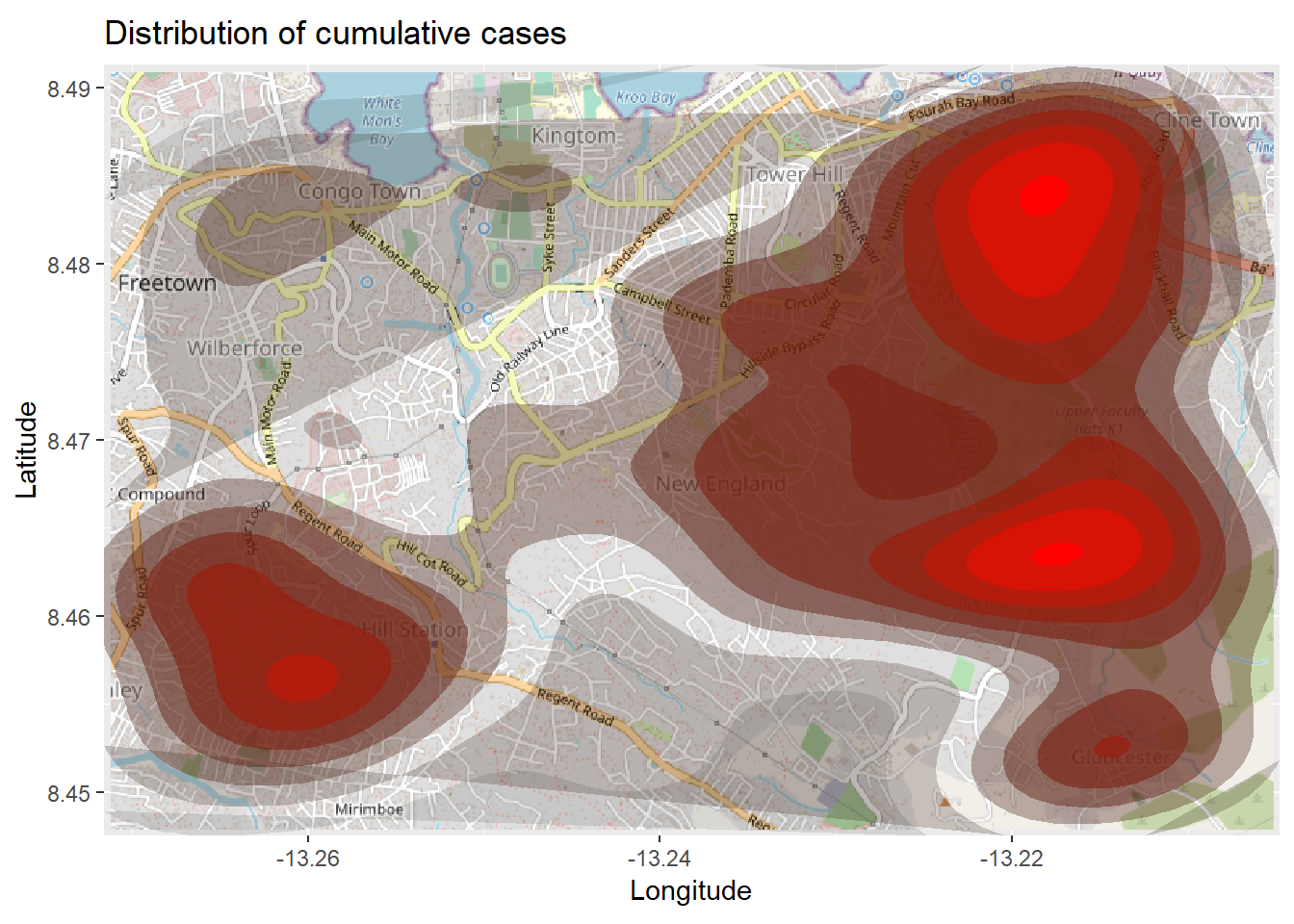
Time series heatmap
The density heatmap above shows cumulative cases. We can examine the outbreak over time and space by faceting the heatmap based on the month of symptom onset, as derived from the linelist.
We begin in the linelist, creating a new column with the Year and Month of onset. The format() function from base R changes how a date is displayed. In this case we want “YYYY-MM”.
# Extract month of onset
linelist <- linelist %>%
mutate(date_onset_ym = format(date_onset, "%Y-%m"))
# Examine the values
table(linelist$date_onset_ym, useNA = "always")##
## 2014-04 2014-05 2014-06 2014-07 2014-08 2014-09 2014-10 2014-11 2014-12 2015-01 2015-02 2015-03 2015-04 <NA>
## 1 10 10 33 89 187 200 119 104 80 44 58 28 37Now, we simply introduce facetting via ggplot2 to the density heatmap. facet_wrap() is applied, using the new column as rows. We set the number of facet columns to 3 for clarity.
# packages
pacman::p_load(OpenStreetMap, tidyverse)
# begin with the basemap
autoplot.OpenStreetMap(map_latlon)+
# add the density plot
ggplot2::stat_density_2d(
data = linelist,
aes(
x = lon,
y = lat,
fill = ..level..,
alpha = ..level..),
bins = 10,
geom = "polygon",
contour_var = "count",
show.legend = F) +
# specify color scale
scale_fill_gradient(low = "black", high = "red")+
# labels
labs(x = "Longitude",
y = "Latitude",
title = "Distribution of cumulative cases over time")+
# facet the plot by month-year of onset
facet_wrap(~ date_onset_ym, ncol = 4)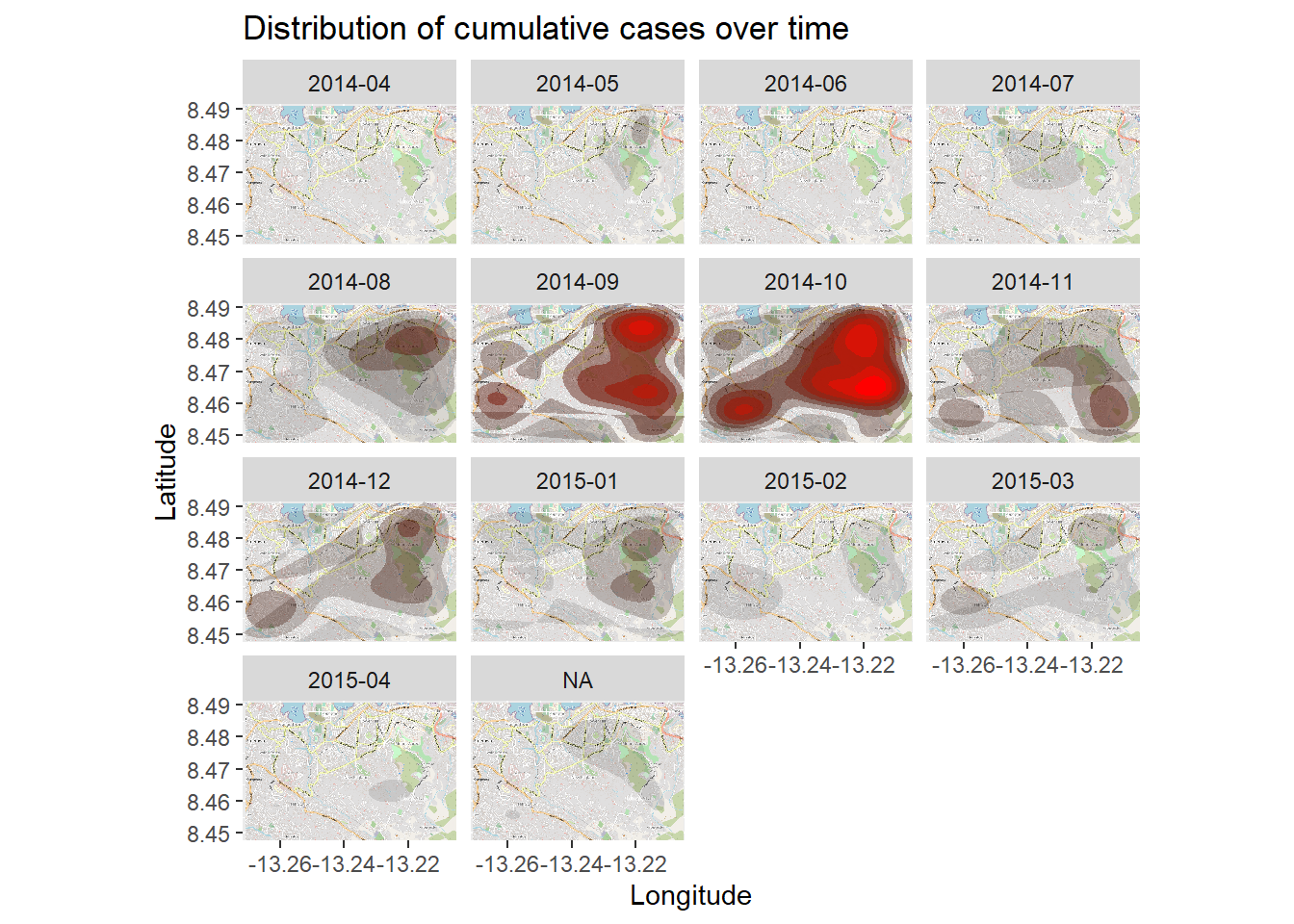 
28.11 Spatial statistics
Most of our discussion so far has focused on visualization of spatial data. In some cases, you may also be interested in using spatial statistics to quantify the spatial relationships of attributes in your data. This section will provide a very brief overview of some key concepts in spatial statistics, and suggest some resources that will be helpful to explore if you wish to do more comprehensive spatial analyses.
Spatial relationships
Before we can calculate any spatial statistics, we need to specify the relationships between features in our data. There are many ways to conceptualize spatial relationships, but a simple and commonly-applicable model to use is that of adjacency - specifically, that we expect a geographic relationship between areas that share a border or “neighbour” one another.
We can quantify adjacency relationships between administrative region polygons in the sle_adm3 data we have been using with the spdep package. We will specify queen contiguity, which means that regions will be neighbors if they share at least one point along their borders. The alternative would be rook contiguity, which requires that regions share an edge - in our case, with irregular polygons, the distinction is trivial, but in some cases the choice between queen and rook can be influential.
sle_nb <- spdep::poly2nb(sle_adm3_dat, queen=T) # create neighbors
sle_adjmat <- spdep::nb2mat(sle_nb) # create matrix summarizing neighbor relationships
sle_listw <- spdep::nb2listw(sle_nb) # create listw (list of weights) object -- we will need this later
sle_nb## Neighbour list object:
## Number of regions: 9
## Number of nonzero links: 30
## Percentage nonzero weights: 37.03704
## Average number of links: 3.333333
round(sle_adjmat, digits = 2)## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
## 1 0.00 0.20 0.00 0.20 0.00 0.2 0.00 0.20 0.20
## 2 0.25 0.00 0.00 0.25 0.25 0.0 0.00 0.25 0.00
## 3 0.00 0.00 0.00 0.50 0.00 0.0 0.00 0.00 0.50
## 4 0.25 0.25 0.25 0.00 0.00 0.0 0.00 0.00 0.25
## 5 0.00 0.33 0.00 0.00 0.00 0.0 0.33 0.33 0.00
## 6 0.50 0.00 0.00 0.00 0.00 0.0 0.00 0.50 0.00
## 7 0.00 0.00 0.00 0.00 0.50 0.0 0.00 0.50 0.00
## 8 0.20 0.20 0.00 0.00 0.20 0.2 0.20 0.00 0.00
## 9 0.33 0.00 0.33 0.33 0.00 0.0 0.00 0.00 0.00
## attr(,"call")
## spdep::nb2mat(neighbours = sle_nb)The matrix printed above shows the relationships between the 9 regions in our sle_adm3 data. A score of 0 indicates two regions are not neighbors, while any value other than 0 indicates a neighbor relationship. The values in the matrix are scaled so that each region has a total row weight of 1.
A better way to visualize these neighbor relationships is by plotting them:
plot(sle_adm3_dat$geometry) + # plot region boundaries
spdep::plot.nb(sle_nb,as(sle_adm3_dat, 'Spatial'), col='grey', add=T) # add neighbor relationships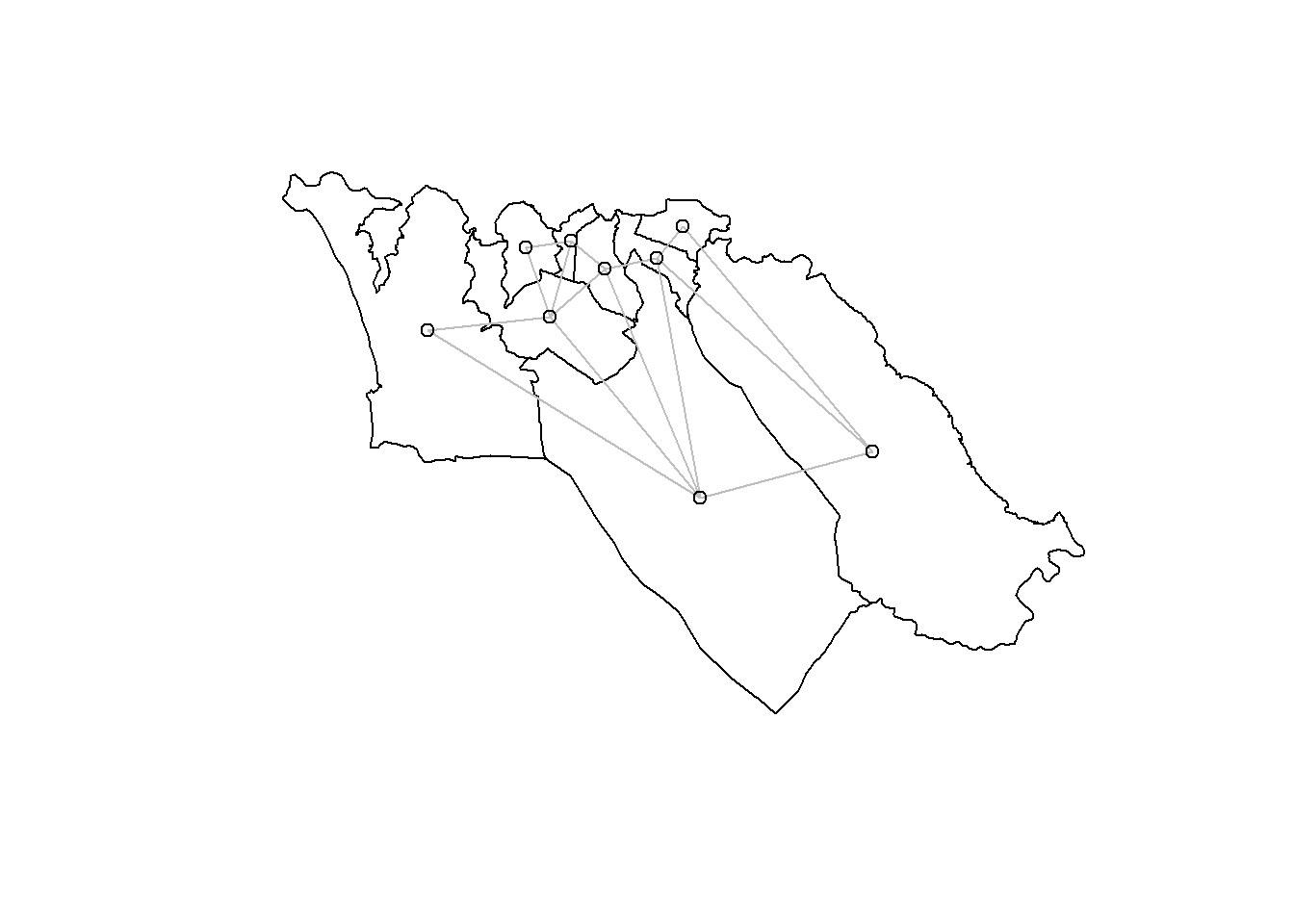
We have used an adjacency approach to identify neighboring polygons; the neighbors we identified are also sometimes called contiguity-based neighbors. But this is just one way of choosing which regions are expected to have a geographic relationship. The most common alternative approaches for identifying geographic relationships generate distance-based neighbors; briefly, these are:
K-nearest neighbors - Based on the distance between centroids (the geographically-weighted center of each polygon region), select the n closest regions as neighbors. A maximum-distance proximity threshold may also be specified. In spdep, you can use
knearneigh()(see documentation).Distance threshold neighbors - Select all neighbors within a distance threshold. In spdep, these neighbor relationships can be identified using
dnearneigh()(see documentation).
Spatial autocorrelation
Tobler’s oft-cited first law of geography states that “everything is related to everything else, but near things are more related than distant things.” In epidemiology, this often means that risk of a particular health outcome in a given region is more similar to its neighboring regions than to those far away. This concept has been formalized as spatial autocorrelation - the statistical property that geographic features with similar values are clustered together in space. Statistical measures of spatial autocorrelation can be used to quantify the extent of spatial clustering in your data, locate where clustering occurs, and identify shared patterns of spatial autocorrelation between distinct variables in your data. This section gives an overview of some common measures of spatial autocorrelation and how to calculate them in R.
Moran’s I - This is a global summary statistic of the correlation between the value of a variable in one region, and the values of the same variable in neighboring regions. The Moran’s I statistic typically ranges from -1 to 1. A value of 0 indicates no pattern of spatial correlation, while values closer to 1 or -1 indicate stronger spatial autocorrelation (similar values close together) or spatial dispersion (dissimilar values close together), respectively.
For an example, we will calculate a Moran’s I statistic to quantify the spatial autocorrelation in Ebola cases we mapped earlier (remember, this is a subset of cases from the simulated epidemic linelist dataframe). The spdep package has a function, moran.test, that can do this calculation for us:
moran_i <-spdep::moran.test(sle_adm3_dat$cases, # numeric vector with variable of interest
listw=sle_listw) # listw object summarizing neighbor relationships
moran_i # print results of Moran's I test##
## Moran I test under randomisation
##
## data: sle_adm3_dat$cases
## weights: sle_listw
##
## Moran I statistic standard deviate = 1.6997, p-value = 0.04459
## alternative hypothesis: greater
## sample estimates:
## Moran I statistic Expectation Variance
## 0.23224301 -0.12500000 0.04417572The output from the moran.test() function shows us a Moran I statistic of round(moran_i$estimate[1],2). This indicates the presence of spatial autocorrelation in our data - specifically, that regions with similar numbers of Ebola cases are likely to be close together. The p-value provided by moran.test() is generated by comparison to the expectation under null hypothesis of no spatial autocorrelation, and can be used if you need to report the results of a formal hypothesis test.
Local Moran’s I - We can decompose the (global) Moran’s I statistic calculated above to identify localized spatial autocorrelation; that is, to identify specific clusters in our data. This statistic, which is sometimes called a Local Indicator of Spatial Association (LISA) statistic, summarizes the extent of spatial autocorrelation around each individual region. It can be useful for finding “hot” and “cold” spots on the map.
To show an example, we can calculate and map Local Moran’s I for the Ebola case counts used above, with the local_moran() function from spdep:
# calculate local Moran's I
local_moran <- spdep::localmoran(
sle_adm3_dat$cases, # variable of interest
listw=sle_listw # listw object with neighbor weights
)
# join results to sf data
sle_adm3_dat<- cbind(sle_adm3_dat, local_moran)
# plot map
ggplot(data=sle_adm3_dat) +
geom_sf(aes(fill=Ii)) +
theme_bw() +
scale_fill_gradient2(low="#2c7bb6", mid="#ffffbf", high="#d7191c",
name="Local Moran's I") +
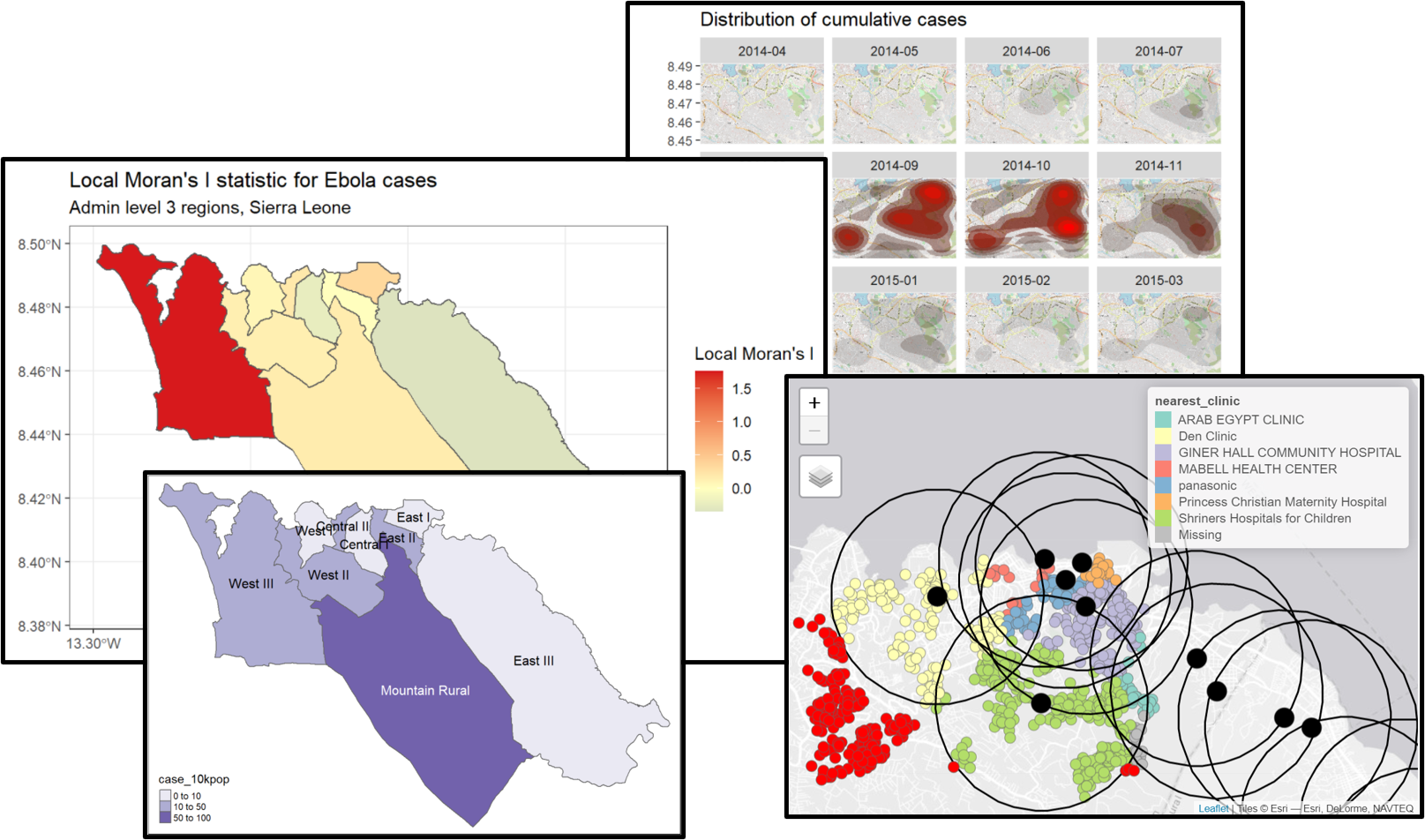
labs(title="Local Moran's I statistic for Ebola cases",
subtitle="Admin level 3 regions, Sierra Leone")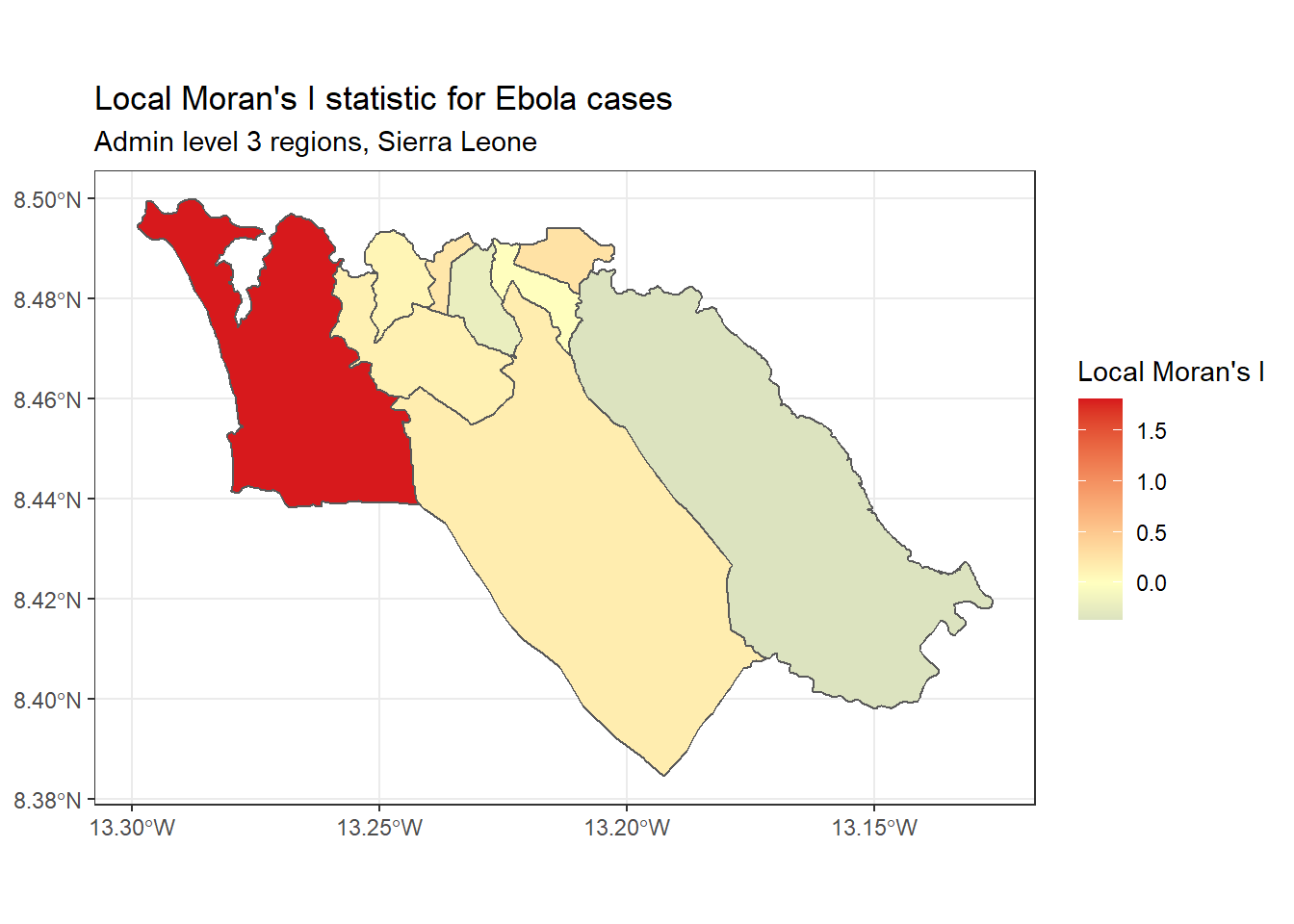
Getis-Ord Gi* - This is another statistic that is commonly used for hotspot analysis; in large part, the popularity of this statistic relates to its use in the Hot Spot Analysis tool in ArcGIS. It is based on the assumption that typically, the difference in a variable’s value between neighboring regions should follow a normal distribution. It uses a z-score approach to identify regions that have significantly higher (hot spot) or significantly lower (cold spot) values of a specified variable, compared to their neighbors.
We can calculate and map the Gi* statistic using the localG() function from spdep:
# Perform local G analysis
getis_ord <- spdep::localG(
sle_adm3_dat$cases,
sle_listw
)
# join results to sf data
sle_adm3_dat$getis_ord <- getis_ord
# plot map
ggplot(data=sle_adm3_dat) +
geom_sf(aes(fill=getis_ord)) +
theme_bw() +
scale_fill_gradient2(low="#2c7bb6", mid="#ffffbf", high="#d7191c",
name="Gi*") +
labs(title="Getis-Ord Gi* statistic for Ebola cases",
subtitle="Admin level 3 regions, Sierra Leone")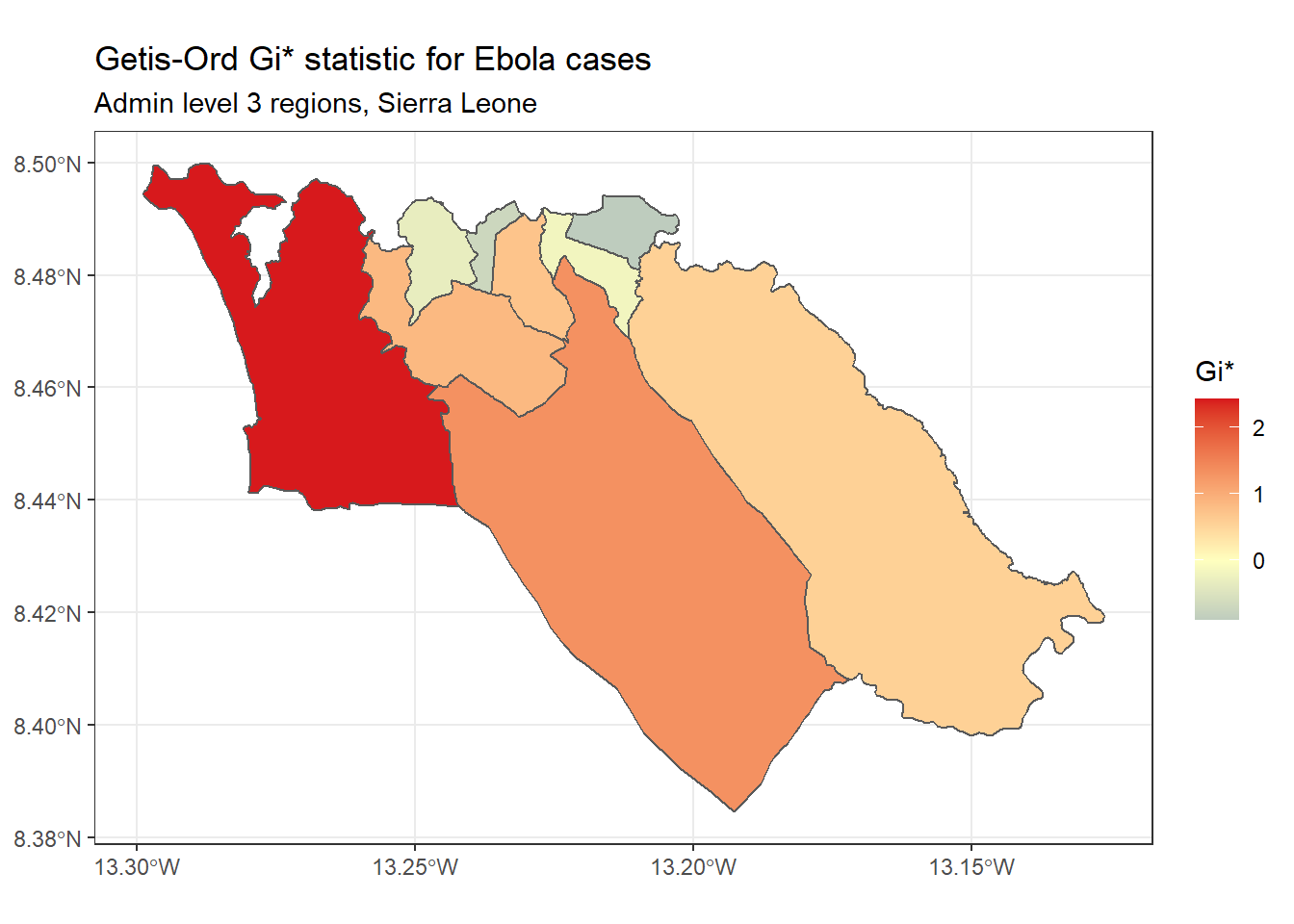
As you can see, the map of Getis-Ord Gi* looks slightly different from the map of Local Moran’s I produced earlier. This reflects that the method used to calculate these two statistics are slightly different; which one you should use depends on your specific use case and the research question of interest.
Lee’s L test - This is a statistical test for bivariate spatial correlation. It allows you to test whether the spatial pattern for a given variable x is similar to the spatial pattern of another variable, y, that is hypothesized to be related spatially to x.
To give an example, let’s test whether the spatial pattern of Ebola cases from the simulated epidemic is correlated with the spatial pattern of population. To start, we need to have a population variable in our sle_adm3 data. We can use the total variable from the sle_adm3_pop dataframe that we loaded earlier.
sle_adm3_dat <- sle_adm3_dat %>%
rename(population = total) # rename 'total' to 'population'We can quickly visualize the spatial patterns of the two variables side by side, to see whether they look similar:
tmap_mode("plot")
cases_map <- tm_shape(sle_adm3_dat) + tm_polygons("cases") + tm_layout(main.title="Cases")
pop_map <- tm_shape(sle_adm3_dat) + tm_polygons("population") + tm_layout(main.title="Population")
tmap_arrange(cases_map, pop_map, ncol=2) # arrange into 2x1 facets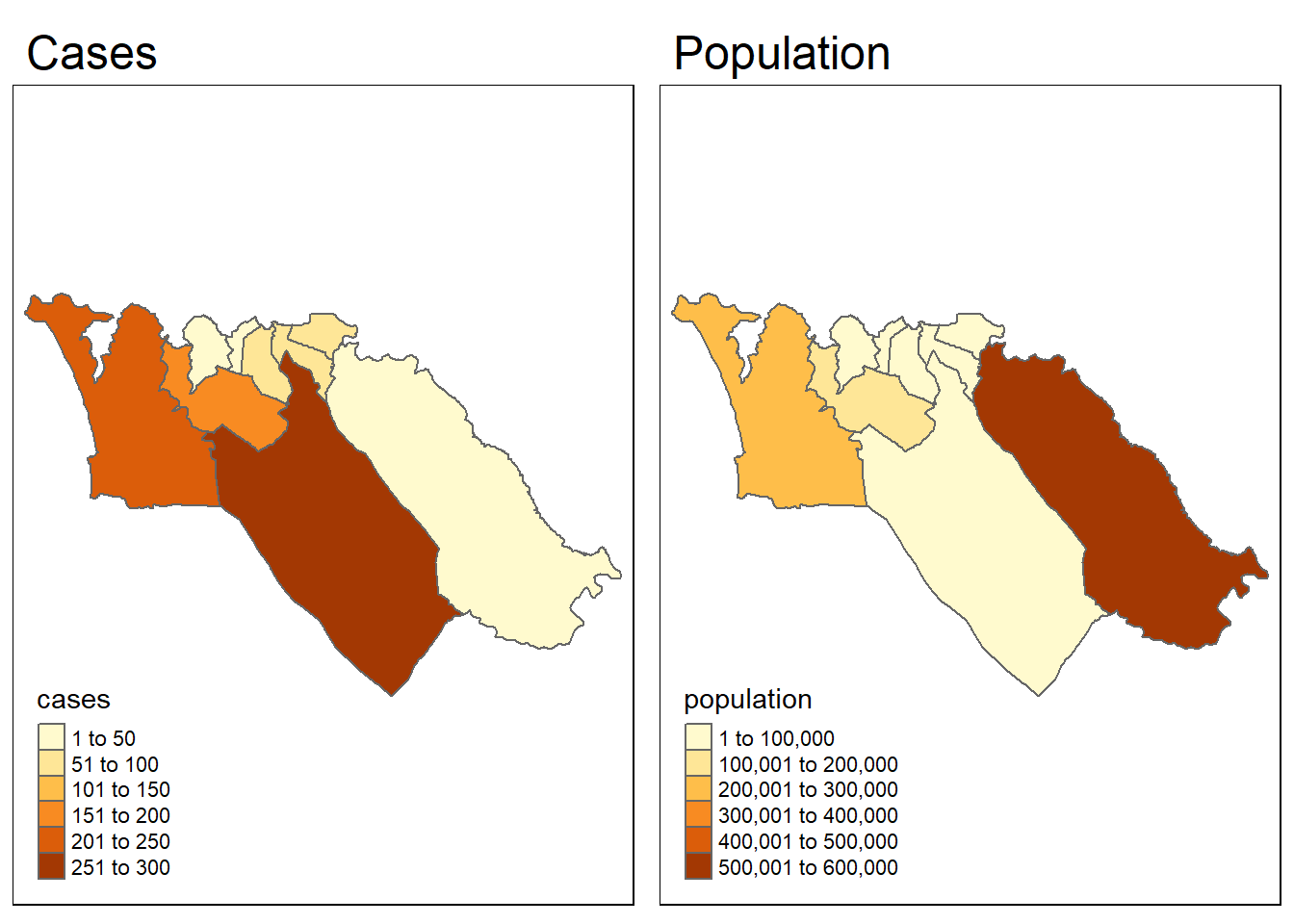
Visually, the patterns seem dissimilar. We can use the lee.test() function in spdep to test statistically whether the pattern of spatial autocorrelation in the two variables is related. The L statistic will be close to 0 if there is no correlation between the patterns, close to 1 if there is a strong positive correlation (i.e. the patterns are similar), and close to -1 if there is a strong negative correlation (i.e. the patterns are inverse).
lee_test <- spdep::lee.test(
x=sle_adm3_dat$cases, # variable 1 to compare
y=sle_adm3_dat$population, # variable 2 to compare
listw=sle_listw # listw object with neighbor weights
)
lee_test##
## Lee's L statistic randomisation
##
## data: sle_adm3_dat$cases , sle_adm3_dat$population
## weights: sle_listw
##
## Lee's L statistic standard deviate = -1.03, p-value = 0.8485
## alternative hypothesis: greater
## sample estimates:
## Lee's L statistic Expectation Variance
## -0.14765600 -0.03325260 0.01233719The output above shows that the Lee’s L statistic for our two variables was round(lee_test$estimate[1],2), which indicates weak negative correlation. This confirms our visual assessment that the pattern of cases and population are not related to one another, and provides evidence that the spatial pattern of cases is not strictly a result of population density in high-risk areas.
The Lee L statistic can be useful for making these kinds of inferences about the relationship between spatially distributed variables; however, to describe the nature of the relationship between two variables in more detail, or adjust for confounding, spatial regression techniques will be needed. These are described briefly in the following section.
Spatial regression
You may wish to make statistical inferences about the relationships between variables in your spatial data. In these cases, it is useful to consider spatial regression techniques - that is, approaches to regression that explicitly consider the spatial organization of units in your data. Some reasons that you may need to consider spatial regression models, rather than standard regression models such as GLMs, include:
Standard regression models assume that residuals are independent from one another. In the presence of strong spatial autocorrelation, the residuals of a standard regression model are likely to be spatially autocorrelated as well, thus violating this assumption. This can lead to problems with interpreting the model results, in which case a spatial model would be preferred.
Regression models also typically assume that the effect of a variable x is constant over all observations. In the case of spatial heterogeneity, the effects we wish to estimate may vary over space, and we may be interested in quantifying those differences. In this case, spatial regression models offer more flexibility for estimating and interpreting effects.
The details of spatial regression approaches are beyond the scope of this handbook. This section will instead provide an overview of the most common spatial regression models and their uses, and refer you to references that may of use if you wish to explore this area further.
Spatial error models - These models assume that the error terms across spatial units are correlated, in which case the data would violate the assumptions of a standard OLS model. Spatial error models are also sometimes referred to as simultaneous autoregressive (SAR) models. They can be fit using the errorsarlm() function in the spatialreg package (spatial regression functions which used to be a part of spdep).
Spatial lag models - These models assume that the dependent variable for a region i is influenced not only by value of independent variables in i, but also by the values of those variables in regions neighboring i. Like spatial error models, spatial lag models are also sometimes described as simultaneous autoregressive (SAR) models. They can be fit using the lagsarlm() function in the spatialreg package.
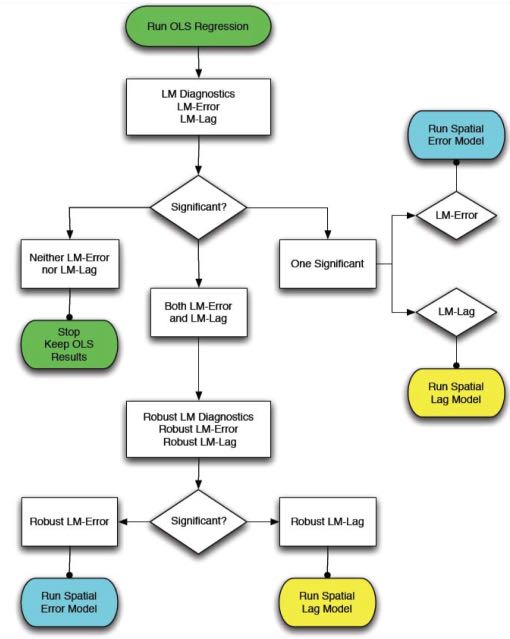
The spdep package contains several useful diagnostic tests for deciding between standard OLS, spatial lag, and spatial error models. These tests, called Lagrange Multiplier diagnostics, can be used to identify the type of spatial dependence in your data and choose which model is most appropriate. The function lm.LMtests() can be used to calculate all of the Lagrange Multiplier tests. Anselin (1988) also provides a useful flow chart tool to decide which spatial regression model to use based on the results of the Lagrange Multiplier tests:
Bayesian hierarchical models - Bayesian approaches are commonly used for some applications in spatial analysis, most commonly for disease mapping. They are preferred in cases where case data are sparsely distributed (for example, in the case of a rare outcome) or statistically “noisy”, as they can be used to generate “smoothed” estimates of disease risk by accounting for the underlying latent spatial process. This may improve the quality of estimates. They also allow investigator pre-specification (via choice of prior) of complex spatial correlation patterns that may exist in the data, which can account for spatially-dependent and -independent variation in both independent and dependent variables. In R, Bayesian hierarchical models can be fit using the CARbayes package (see vignette) or R-INLA (see website and textbook). R can also be used to call external software that does Bayesian estimation, such as JAGS or WinBUGS.
28.12 Resources
R Simple Features and sf package vignette
R tmap package vignette
Spatial Data in R (EarthLab course)
Applied Spatial Data Analysis in R textbook
SpatialEpiApp - a Shiny app that is downloadable as an R package, allowing you to provide your own data and conduct mapping, cluster analysis, and spatial statistics.
An Introduction to Spatial Econometrics in R workshop